0 引言

在上1 期里，您已经领会( 理解)Encoder 的涵意和功能了。在本期里，就继续来领会Decoder 的涵意和功能。由于这两者是息息相关的。例如在Diffusion 模型里，就含有文本编码器(text encoder)、图像编码器(image decoder)、以及(decoder) 等。

于是，当您已经深入理解编码器了，就能轻易继续理解另一名词：(Decoder)。兹回忆上1 期的说明：Encoder 负责从有招的世界，萃取( 过滤)& 沉淀于无招世界( 即AI 的潜藏空间)，然后由Decoder 来生成千变万化的新招式。例如，上1 期所举的< 换脸> 范例( 图1)。

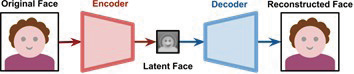
图1

图片来源：https://arxiv.org/pdf/1909.11573.pdf

您已经理解Encoder了。接下来，我们就来详细说明Decoder是如何< 生成>( 无中生有) 呢?

1 Decoder如何生成?

Decoder 的无中生有技能是它经由机器学习(Machine Learning) 过程，而获得的知识和智能；基于这学来的智慧来进行< 生成>。我们先从简单的例子出发。例如，让它( 即Decoder) 学习：< 输入1 个数值--1，而输出3 个数值( 红色RGB 的数值) -- [255, 0, 0]。兹以图2 表示。

图2

然后继续让学习更多。例如学习：< 输入一个数值--100，而输出3 个数值( 绿色RGB的数值) -- [0, 255, 0]。并且学习：< 输入1 个数值-- 200，而输出3 个数值( 蓝色RGB的数值) -- [0, 0, 255]。共学习了3项智能(图3)。

图3

俗语说：学而时习之。让它重复学习更多回合，它就掌握上述的3 项生成< 规律> 了。之后，只要我们输入^[1]给这Decoder，它就会生成很接近于[255, 0, 0]的值，但不一定是[255, 0, 0]。同样地，只要输入[100]给这Decoder，它就会生成很接近于[0, 255, 0] 的值，但只是近似而已。

请您想一想：此时如果您输入一个值[95] 给这Decoder，那么它会输出什么值呢? 这只是一个起点，逐渐地扩大Decoder 的能力，就能做出形形色色的图像生成了。例如，从上述范例的输出都是1 个点的颜色RGB 值。我们可以扩大输出( 生成)，例如输出4 个彩色点的RGB 值。每一个点都有RGB 3 个值，而4 个点共有12 个值。也就是输出1 个向量，其含有12 个值(图4)。

图4

继续让它学习更多种配对(图5)。

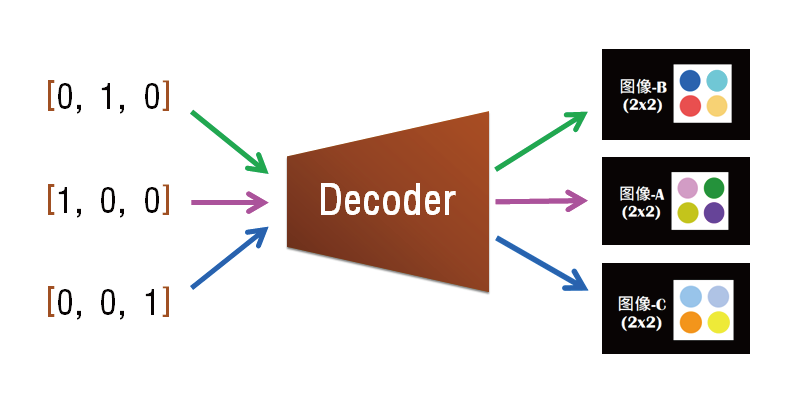
图5

接下来， 还可以扩大输出( 生成)， 例如输出128x128 彩色点的RGB 值。每一个点都有RGB3 个值，共有128x128x3 个值。也就是输出1张JPG图像( 图6)。

图6

然后请试想：此时如果您输入一个向量值[0.1, 0.1,0.9] 给这Decoder，那么它会生成什么图像呢?

2 Decoder的生成智慧从哪里来?

以上说明了Decoder 经由数千或数万回合的重复学习，而学习其对应规律，而拥有生成的技能。而人们透过输入值来引导它生成不同色彩、形状的图像。在上述的说明中，请您勿必留意：人们输入值〔0, 1, 0〕等只是用来引导Decoder 去微调其所学的知识，来绘出作品。就如同学生问老师时，从古典的角度而观之，是老师在帮学生解析问题。其实也是：学生在引导老师去表达其深厚的学问。

所以，Decoder 不是去解析人们的输入数据，而是Decoder 参考人们的输入( 指引)，来微调Decoder 的所学，而进行生成作品。亦即，AI 不是传统IT 系统依循人们所写的程序逻辑去创作，而是依其自己所学习的规律去进行生成。例如，AI 重复观察Picasso 数百张画作之后，学会了Picasso 的颜色风格( 规律)，AI 就会依循其所学的规律来渲染张大千的画作。

再举例说明之，例如有一位妈妈经过许多年学会做早餐便当。今天一早，她的小孩告诉她说：今天便当加个苛包蛋。她就依其小孩指引开始准备便当。她在准备便当的过程中，又听到其小孩说：蛋不要太咸。于是她就微调，而做出了一个：不咸荷包蛋的早餐便当。

小孩在两个时间点提供指引：1 个是创作前，1 个是创作中。妈妈也可要求小孩提供更多指引，例如妈妈说：请您给我看看其他同学的便当内容照片。于是她就依循其他同学便当特色来微调脑海中便当的景像，而做出1 个更符合小孩口味的便当。这里也要很留意：她就依循其他同学〈便当特色〉来微调脑海中便当的景像。只是提取特色而已，而不解析其细节。

3 Decoder内部的NN模型

刚才的范例说明了：人们输入值〔0, 1〕等只是用来引导Decoder 去微调其所学的知识，来绘出作品。现在继续来看看Decoder 的内部结构。无论是Encoder 或Decoder，其内部都是一个简单的计算公式： Y = X *W + B。兹以图表示之( 图7)。

图7

看看Decoder内部的神经网络(NN：Neural Netwoks)架构( 图8)。

图8

这结构里含有w[ ] 数组，和b[ ] 向量，也就是AI模型的参数。以图9 表示之。

图9

其中的计算关系是：

●   当我们输入X=[1,0]，经由Y = X*W+B 的计算，就输出Y=[255, 0,0]；

●   当我们输入X=[1,1]，经由Y = X*W+B 的计算，就输出Y=[0, 0, 255]；

●   当我们输入X=[0,1]，经由Y = X*W+B 的计算，就输出Y=[0, 255, 0]。

请您试想，上图里的w[ ] 和b[ ] 为何，才能同时满足上述的3 项计算呢? 其答案并不是唯一的。亦即，可能有好几组 W&B 可以满足上述的要求。例如，可以透过机器学习，来找到一组< 同时> 满足上述3 项的计算( 图10)。

图10

当我们输入X=[1,0]，经由Y = X*W+B 的计算，就输出Y=[255, 0,0]。

其计算过程为：

● y0 = x0 * w00 + x1 * w10 + b0 = 1*0 + 0*-255 +255 = 255；

● y1 = x0 * w01 + x1 * w11 + b1 = 1*-255 + 0*0 +255 = 0；

● y2 = x0 * w02 + x1 * w12 + b2 = 1*255 + 0*255 -255 = 0 。

于是就输出了：[255, 0, 0]。同理， 当我们输入X=[1,1]，经由Y = X*W+B 的计算，就输出Y=[0, 0,255]。而且，当我们输入X=[1,1]，经由Y = X*W+B 的计算，就输出Y=[0, 0, 255]。以图11 表示之。

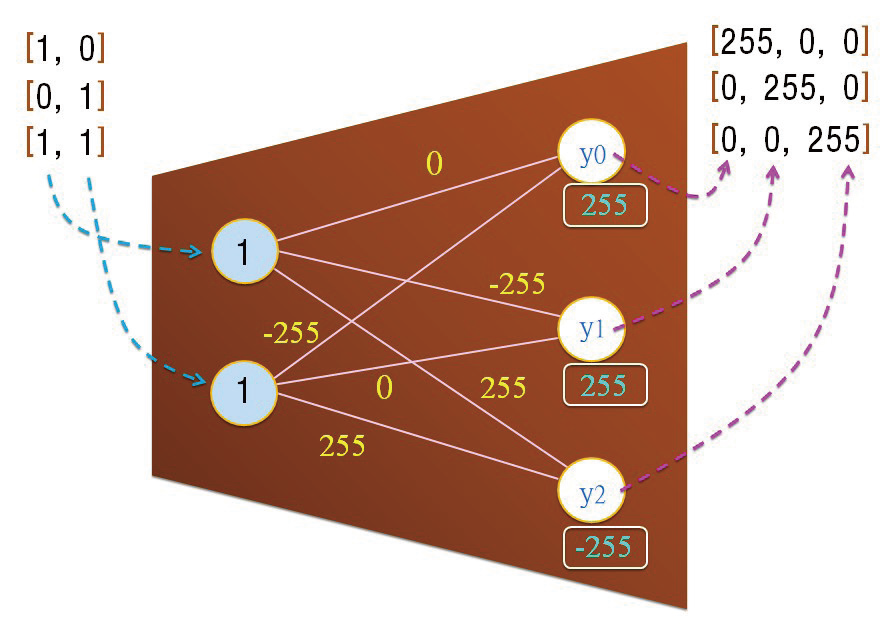
图11

于是，这是完美的一组W&B，能同时满足上述的3项对应规律。所谓< 机器学习>，或< 训练模型> 就是AI 在找寻一组完美的W&B。

4 结束语

为了简单易懂起见，上述的Decoder 都是单层NN架构而已。然而一般的Decoder 都是深度NN 架构( 即含有多个隐藏层)。还有，像Stable Diffusion 在Encoder与Decoder 之间，又添加了更多隐藏层的计算，强化的创新组合能力，来生成更丰富的内容。

（本文来源于《电子产品世界》杂志2023年7月期）