近年来，随着太赫兹技术的发展，太赫兹调频连续波雷达物位计的研究已经广泛开展。太赫兹波是指频率范围为0.1-10THz的电磁波，与微波、毫米波相比，其波长短且带宽大，应用于雷达方面具有高距离分辨率，无盲区、低截获率及强抗干扰能力等众多优势。由于太赫兹雷达的频率较高，采用调频连续波(frequencymodulatedcontinuouswave，FMCW)雷达体制，将高频的发射和回波信号转换成低频的差频信号，便于信号处理。在信号处理中采用快速傅里叶变换(fastFou-riertransform，FFT)的方法分析差频信号频谱，存在着频谱泄露和栅栏效应，影响其频率估计精度。比值法是利用峰值谱线和相邻谱线的比例关系估计频率，但在噪声环境下频率估计精度不高。能量重心法通过加窗函数减少频谱泄露，但选取点数少，估计精度较低。结合比值法和能量重心法，并对FFT结果做线性组合代替窗函数减少了计算量，提高了精度，但在信号非整周期截断时，频谱泄露使精度提高有限。

本文主要根据差频信号的特点，综合考虑测量误差和实时性的要求，提出一种提高太赫兹调频连续波雷达物位计测量精度的算法，此算法首先通过调整采样参数实现整周期采样，然后利用峰值谱线的相邻谱线的梯度关系调整确定主瓣中心位置，估计实际频率。本算法在Matlab中进行了仿真实验，实验结果表明该算法易于实现，太赫兹调频连续波雷达物位计测量精度比直接FFT高很多，与比值法和能量重心法相比有所提高。

1、太赫兹调频连续波雷达物位计结构与测距原理

①太赫兹调频连续波雷达物位计结构

太赫兹调频连续波雷达物位计如图1所示，数字信号处理器产生三角波，控制压控振荡器产生高频连续波发射信号，经过放大器和天线发射出去，同时经过功分器将一部分发射信号送入混频器中作为本振信号。发射信号遇到目标后散射回来经接收天线和低噪放大器进入混频器中，与本振信号混频后产生较低频率的差频信号，其中包括所需的距离信息和无关的干扰信号，A/D采样之后通过数字信号处理器完成目标距离信息的提取。

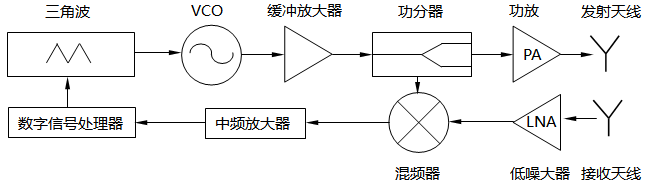
图1 太赫兹调频连续波雷达物位计结构示意图

②太赫兹调频连续波雷达物位计测距原理

太赫兹调频连续波雷达物位计主要采用三角调频连续波，发射信号经过目标散射之后，被天线接受，延迟时间τ=2R/c，其中R为目标到天线的距离，c为电磁波的传播速度。在探测目标静止情况下，距离计算公式为R=(cT/4B)×fb，公式中T为三角波的周期，B为调频带宽。由公式R=(cT/4B)×fb可得差频信号频率fb与距离R是线性关系，因此，测距系统的关键在于测量差频信号的频率。在带宽B和周期T一定的条件下，只要得到频率fb就可以计算距离R，所以频率测量的精度直接影响测距的精度。差频信号通常经过A/D采样之后利用FFT计算得到N点的离散频谱，然后通过频谱峰值频率得到fb，由于离散频谱会存在频域采样间隔△f=fs/N。公式中fs为采样频率，N为采样点数。经过FFT得到的离散频谱采样一般不能采集到信号频率峰值点，即频率间隔的整数倍与峰值点不重合，导致FFT分析的结果与实际频率不一致，造成频率估计误差。

2、本文所提的方法

本文所提的方法主要经过整周期采样调整和谱线梯度校正两部分来完成，其实现流程如图2所示。

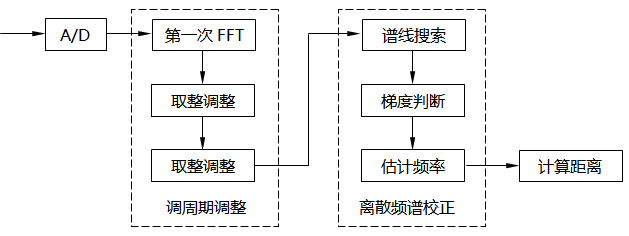
图2 文中所提方法实现流程图

①整周期采样调整

整周期采样调整主要通过三个步骤实现：第一步进行差频信号频率的粗略估计。首先，根据系统的要求确定信号的第一次采样频率fs和采样点数N，保证采样点数是2的幂次方，利于FFT计算。然后经过FFT，根据离散频谱峰值谱线粗略估计差频信号的频率f1;第二步进行采样参数调整值的计算。首先根据频率f1和采样频率fs计算采集信号的单位周期的采集点数a=fs/f1;然后利用采样点数N和单位周期采集数a计算采集的信号周期数b=N/a;随后利用取整函数进行截尾取整得到整周期的信号周期数c=[b];保证采样点数N不变，计算新的单位周期内采样点数d=N/c;最后得到新的采样频率fs=df1。第三步是根据新的采样频率fs和采样点数N对差频信号进行重新采样，新采集到信号基本满足整周期采样的要求，然后通过频谱分析估计差频信号的频率。

②谱线梯度校正法

谱线梯度校正法首先对差频信号进行FFT处理，得到信号离散频谱X(k)，然后利用公式fpeak=argmax[X(k)]得到峰值谱线频率，但是由于误差的存在，峰值谱线的频率与差频信号的实际频率一般不一致。在图3中，假定离散峰值谱线的序号为m，则峰值谱线频率为fpeak=m×△f，其中Δf定义如式△f=fs/N所示。峰值谱线左右相邻两条谱线分别表示为fL=(m-1)×Δf和fH=(m+1)×Δf，相应谱线的幅值分别为X(m-1)和X(m+1)。利用峰值谱线左右相邻谱线的横纵坐标的比例关系，可以构建峰值谱线处的梯度值为r=[X(m+1)-X(m-1)]/(fH-fL)，然后利用r值的正负来调整频率范围，步骤如下：如图3(a)所示，当r>0时，峰值谱线处梯度值大于0，实际谱线峰值位于该谱线峰值的右侧，调整令fL=fpeak和fH=(m+1)×Δf;如图3(b)所示，当r<0时，峰值谱线处梯度值小于0，实际谱线峰值位于该谱线峰值的左侧，调整令fL=(m-1)×Δf和fH=fpeak，则调整后的峰值谱线频率为fpeak=(fL+fH)/2，最后差频信号实际频率值为fb=fpeak。

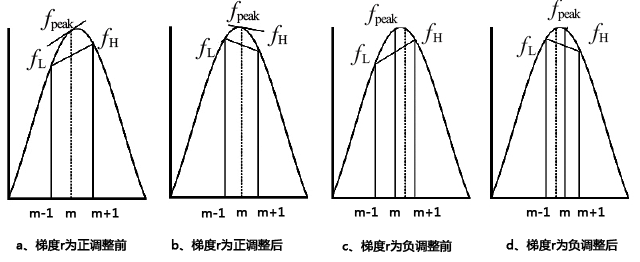
图3 谱线梯度校正图

3、仿真与结果

分析本文在Matlab中进行了仿真验证，实验设定的相关参数：三角波的周期为T=2ms，初始频率f0=10GHz，带宽B=1.5GHz，采样频率fs=200kHz，采样点数N=512，测距范围为1-9m之间。采用直接FFT法作为对比，分别采用比值法、能量重心法和文中的方法进行距离测量。表1中列出了四种方法的在不同距离上的测量误差值。本文的方法在不同的距离上测量偏差是最小的，最接近理论值。比值法由于噪声影响，会导致插值方向出现错误，在某些距离上测量误差比直接采用FFT的大，能量重心法采用的是三点卷积，由于增加了加窗运算，减少了噪声的影响，精度有所提高。

表1 四种方法的距离测量误差对比

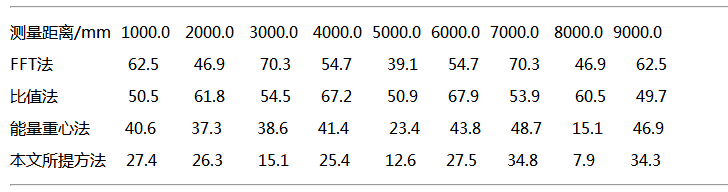
图4显示了四种方法在不同距离上的测量误差的对比情况，本文的方法在不同的距离上相对于其他三种方法测量误差都是最小的。表2列出了三种改进方法的在不同距离上的精度提高程度，在9个测量点上，比值法的精度提高程度平均为2.5%，而能量重心法的精度提高程度平均为30.4%，本文的方法在距离测量精度上有了进一步的提高，平均提高了58.8%。

表2 三种改进方法相对FFT法的测量精度改进程度

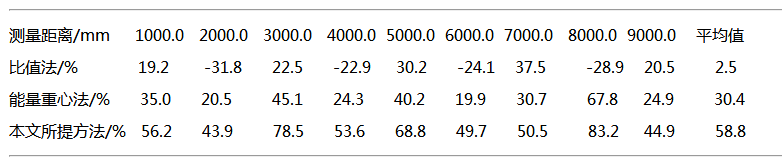
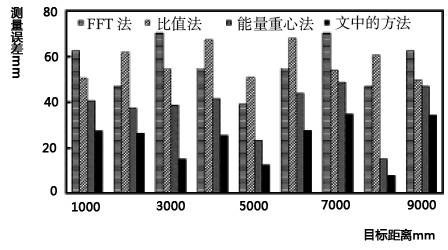
图4 四种方法在不同距离上的误差对比

本文提出了一种提高太赫兹调频连续波雷达物位计测量精度的算法，该算法将整周期采样和谱线梯度校正相结合来测量差频信号频率，首先通过调整采样参数，使得采样序列满足整周期采样要求，减少截断误差对频率精度的影响，然后采用谱线梯度校正来减少离散频谱栅栏效应的影响，通过两步调整提高距离测量精度。实验结果表明：该方法的距离测量精度高，相对于传统的频率估计方法，测量误差最小，与直接采用FFT的方法相比，测量精度平均提高了58.8%，同时此算法实现简单，运算量小，非常适合实时性高的雷达物位测量系统。