一、典型的运动控制系统的架构

工程实践中，大多数控制系统为运动控制系统，比如飞机控制，其实就是通过控制飞机的几个翅膀进而调解作用在飞机上的气动力来调整飞机的姿态。飞机的翅膀上面（舵面）都安装有作动器（简称舵机），通过作动器的位置控制就可以控制舵面的位置，最终实现飞机的控制。

我们一般都会见到如下的一个典型的控制框图，即通过三个环路来实现位置控制（以电机作为最终的出力元件）。外环为位置环，中间为速度环，最内部为电流环，很多第一次接触这种控制方式的人都会多多少少有点疑问：为什么是这是三个环路？换一个行不行？

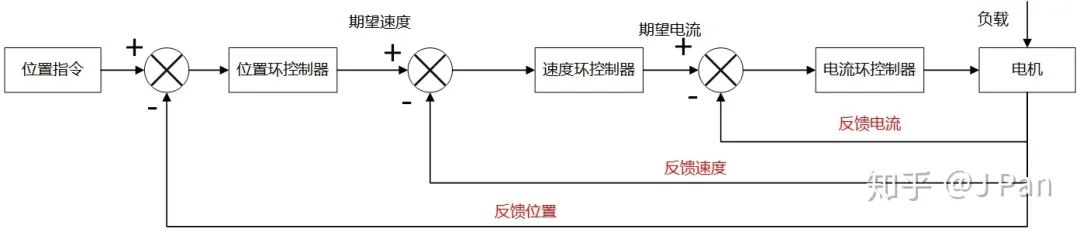
好了，如果我们将上面的环路稍微变形一下，可能会有助于大家的理解：

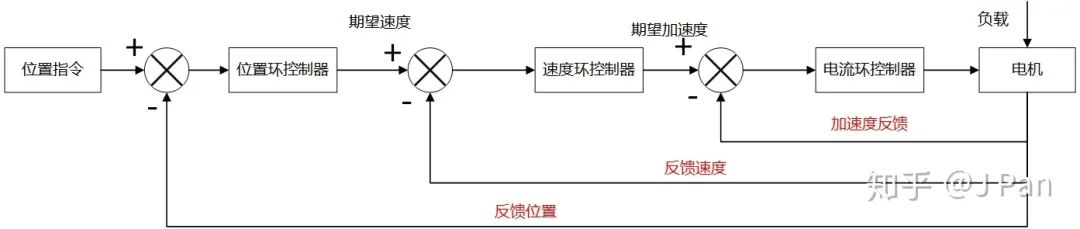
即最内环换成了加速度环，细心的童鞋可能已经注意到了某种规律——位置、速度、加速度，内环是外环的导数？这貌似是有那么一点点规律！——其实呢内环电流环和加速度环是等价的，因为对于理想电机而言，其转矩和电流成正比（比例就是转矩系数），转动惯量可近似认为是常值，这样加速度就和电流成正比，因为电机中电流更容易测量，所以呢一般用电流环来代替加速度环。

好了，那怎么理解这三个环路呢？为什么位置换控制器的输出就是速度环呢?输入呢？——可以这么简单的理解：要想控制位置，可以通过调节速度来实现，因为速度随时间的积分就是位置，合适的速度经过一定的时间就能达到想要的位置；同样，速度可以通过调节合适的电流来实现；那么怎么调节电流呢？

——调节电压啊，怎么调节电压呢？——逆变器啊！好了，是不是知识点都串起来了？——我们先简单的了解一下，后面再进行理论分析。

二、如何设计一个直流电机电流环

先以简单的直流电机为例，一个典型的直流电机的数学模型如下：

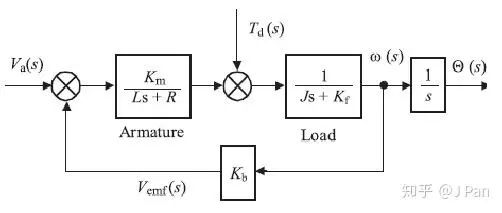
所以电流环的的一般控制模型为：

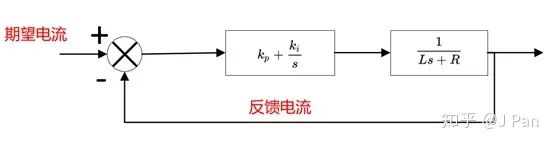
我们画个伯德图看一下这个系统的响应是多少！

figure('color','w');
H = tf([1e6],[1 1500 1e6]);
bode(H);
grid on;

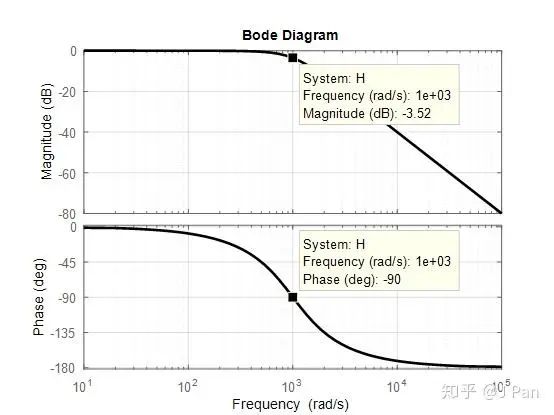
可见在1000rad/s时系统的幅值衰减到-3.53dB，相位滞后90°。

figure('color','w');
H = tf([1450 1e6],[1 1500 1e6]);
w=logspace(2,4,10000);
bode(H,w);
grid on;

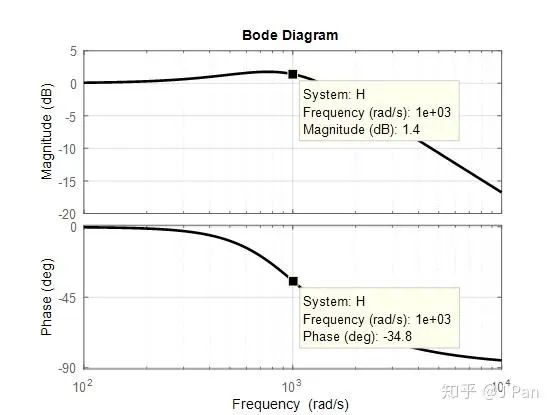
可见，有零点之后1000rad/s时幅值响应为1.4dB，相位响应为-34.8°，和无零点的简化模型有区别，但是主要特征没有发生明显变化，为简单期间呢，我们一般都会用无零点的模型进行控制器设计。

同时注意到，有零点的模型在截止频率附近幅值响应是大于0dB的，也就是大于1的，因此可以预见，系统的响应会出现一定的超调，我们不妨搭个simulink模型看看：

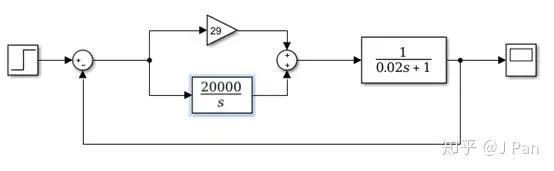
当指令是阶跃指令时，可以看到响应非常快，同时又一定的超调。

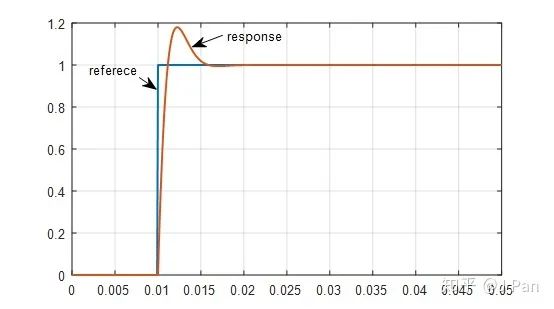
三、什么是积分饱和

在一文中，我们说了，一个系统的截止频率越高，能通过的信号的带宽就越大，这样系统的响应就约快速、越及时，响应时间就越短。理论上只要我们设定了想要的截止频率和阻尼比 ，我们都可以设计一个控制器进行整定，已达到我们设定的带宽——等等，这好像和我们的常识有悖啊，没听说过哪个系统的带宽可以无限宽啊！

问题在哪呢？——首先我们前面的理论分析完全没有问题，理论上截止频率确实可以达到无限宽，但有一个前提，那就是我们要有一个能力无限大的电源！如何理解这句话？

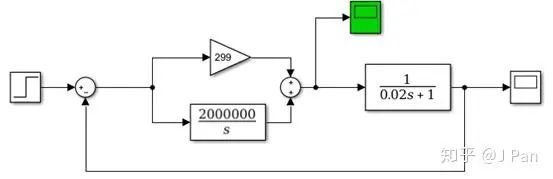
我们把PI控制器的输出显示出来，上图中绿色示波器位置。

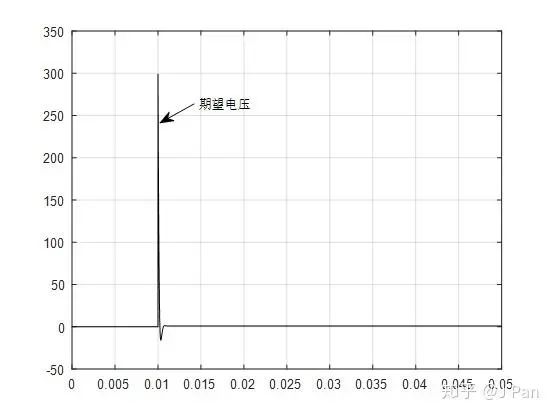
可以看出，为了达到较高的截止频率，需要给绕组的电源电压达到了接近300V，如果想提高截止频率，这个值还会更高，而我们一般的供电电压可能只有28V，那怎么办呢？我们需要在PI控制器后面加一个限幅，如下图所示：

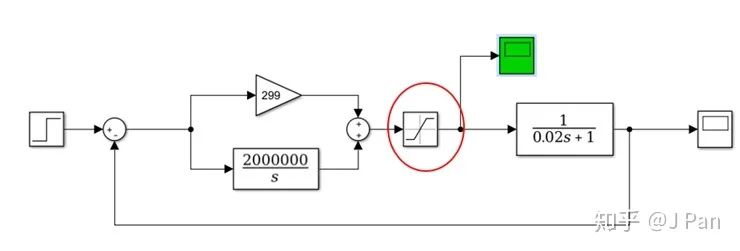
我们以为皆大欢喜了，可是我们计算完后又发现了问题，那就是加完限幅后系统出现了大的超调，如下图所示，这是什么原因呢？

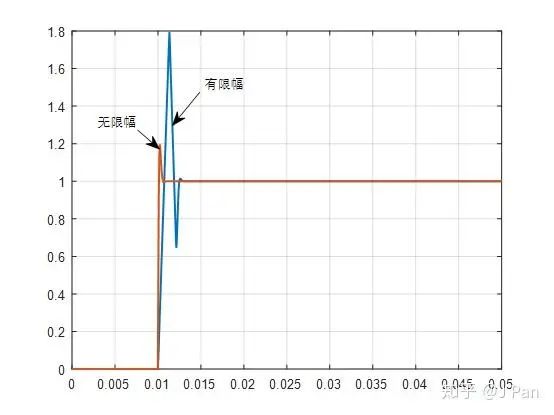
原因也很简单，那就是积分器输出饱和了！——什么意思？请看下图，红色线为原始的PI控制器输出，因为限幅，其实际的输出为绿色线所示（红色和绿色线纵坐标在右侧，蓝色线纵坐标在左侧）。在电流（蓝色线）到达理论值前，由于误差一直是正值，因此积分器不断积分，数值也不断增大，直到到达理论值时积分器达到达最大值，而这个值和限幅相比大的多（800比28）。在电流超过理论值后，误差开始变为幅值，积分器的数值开始减小，但由于之前的数值太大了，需要一段时间后才能减小到零甚至幅值，在到零之前积分器还是正值，而且大部分时间都是很大的值，因此限幅后的PI控制器在电流到达理论值后还会维持一段时间的正值（见绿色线），导致电流出现了较大的超调，这种情况一般叫迎风超调（windup）。

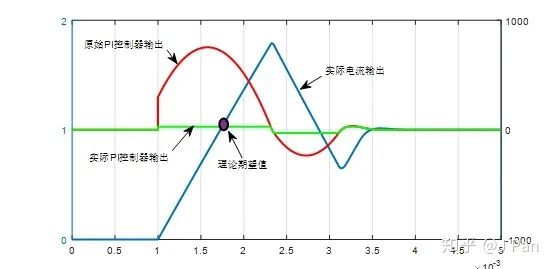
那怎么解决呢？——是不是可以减小PI控制器的积分增益呢？当然是可以的，但这样会导致响应变慢，减小带宽。一个最常见的方法就是采用抗积分饱和的方法（anti-windup），抗积分饱和的方法有很多种，比如积分遇限消弱法(clamping)、积分分离法以及反馈抑制抗饱和法以及变种等，我们简要介绍一下反馈抑制饱和法。

反馈抑制饱和法的采用反馈的基本思想：当饱和时，对积分项加入负反馈，使其尽快退出饱和，具体实现见下图：

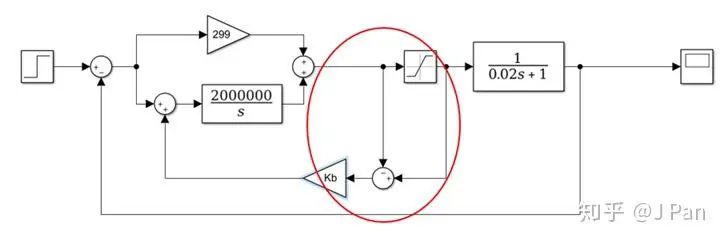
对积分回路增肌负反馈环节，即当积分器积分量较大时，通过负反馈减小其积分值，确保其在一定的范围内。进行积分抑制饱和后其电流的实际响应见下图所示，可见响应时间略慢（因为电压限幅了），但是也没有出现较大的超调。

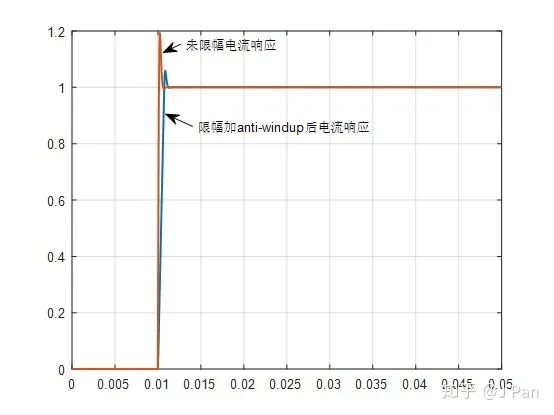
前面分析的都是理论情况，实际上还要复杂一点，比如PI控制器的输出要经过一个计算周期才能更新一次，PWM计算模块计算的三极管门信号最大可能延迟一个斩波周期，逆变器（比如IGBT）从接收到信号到管子作用也要一个时间，以及反馈电流的采集、滤波都有延迟时间，这些要么是延时环节，要么是惯性环节，都会影响带宽，引入这些环节的电流环设计与前面所述的方法是一致的，只是略复杂一点（即将这些量与绕组一起等效成一个大的惯性环节）。当然，一般这些量与电机的电气时间常数  相比都比较小，大多数情况下为简单期间可以先忽略。

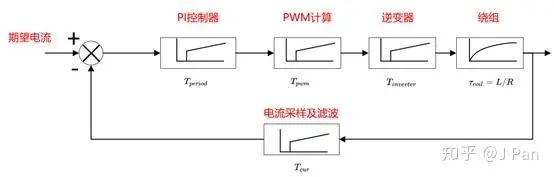
四、如何设计速度环

有了电流环，我们就可以设计速度环了，完整的速度环框图如下图所示：

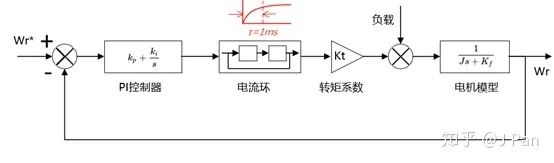
因为电信号的变化是非常快的，电机的电气时间常数一般比机械时间常数小的多，通常我们将电流环的截止频率设计的尽量高，速度环的截止频率要低一些。

在速度环里，因为机械时间常数比电气时间常数大的多，也就是说在一个电气时间常数里面，电机的速度可以认为是不怎么变的，也就是说为简单起见，在速度环里，电流环可以认为响应非常快，可以忽略掉，从而简化成如下结构：

同样我们也加上积分反馈抑制饱和，完整simulink模块如下：

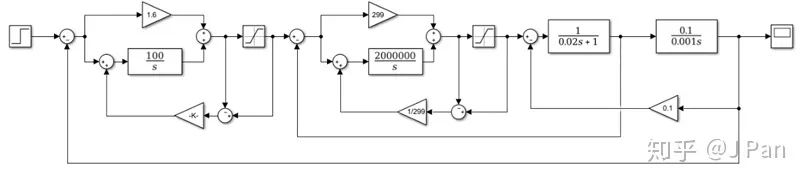
其电流响应曲线和速度响应曲线如下：

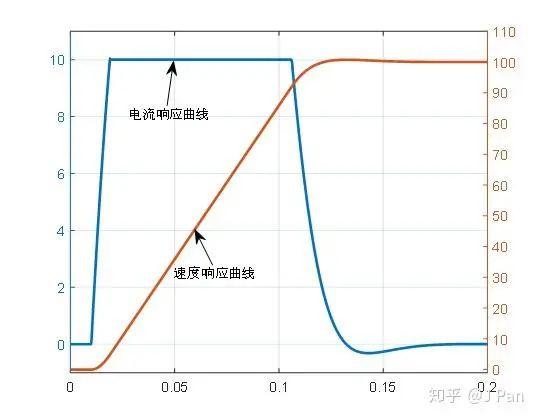
可见，最开始的时候，电流迅速达到设定的最大值，使电机达到最大速度，电流的稳定时间明显比速度小，结束的时候，电流也迅速下降实现制动。

五、如何设计位置环

有了电流环和速度环，相信大家应该已经会设计位置环了。

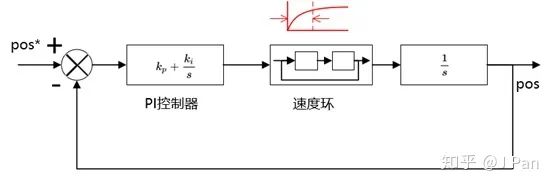
同样，假定位置环的截止频率小于速度环，忽略速度环的响应时间，则系统可简化为：

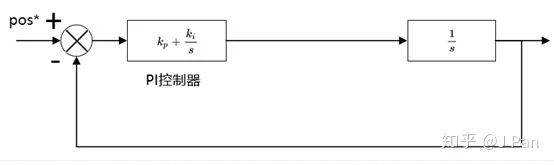
怎么样，简单吧，那就拿simulink自己试试吧，别忘了积分饱和哦。