微波频段介电特性的测量具有重要意义，几种典型需求场景如下：1. 拟基于某介质基板材料实现微带滤波器或谐振器、贴片天线等电路时，需要知晓其介电特性来完成器件/天线的初始设计，然后通过电磁仿真进行优化；2. 机载雷达系统或基站天线系统的天线罩对微波信号的传输有一定的影响，产品设计阶段也需要知晓天线罩材料的介电特性，从而评估天线罩对系统性能的可能影响；3. 在室内定位、穿墙雷达、移动通信信道建模等情景中，建筑材料的介电特性对微波信号的反射、衰减及时延会影响到应用系统性能，而建筑材料的介电特性及其几何结构则是影响微波信号的关键参数，因此也需要评估介电特性。还有许多其它需要评估介电特性的场景，这里不再赘述。

材料的介电特性与通常所说的相对介电常数有所区别，一般地，材料介电特性用复介电常数表示，而相对介电常数是复介电常数的实部。实际应用中，出于方便考虑，材料介电常数通常相对于真空介电常数进行归一化（参见《微波电子学——材料电磁参数的表征与微波测量技术》公式1.15）：

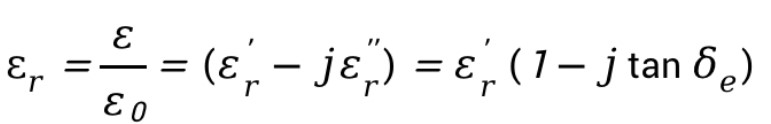
这里，复介电常数可表示为实部-虚部的形式，也可以用相对介电常数和损耗正切来表示。从上式可以看出，复介电常数虚部与损耗正切的关系为

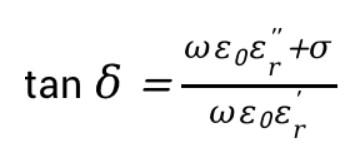
举例：设相对介电常数为4.3、损耗正切为0.025，则复介电常数虚部为4.3*0.025=0.1075。复介电常数的虚部通常是指电介质中由于偶极子振动阻尼而产生的热损耗（参见《微波工程》，张肇仪 等译，第三版8页）。如果需要考虑材料电导率σ引起的损耗，则可以将电导率并入损耗正切中一并考虑（参见《微波工程》，张肇仪 等译，第三版9页）。通常，在电磁仿真软件中，设定材料损耗特性时，要么指定损耗正切，要么指定电导率。容易被忽略的一点是：材料介电特性通常与工作频率有关。因此，对于窄带应用系统，需要确准系统工作频点是否与查阅的材料介电特性频点相对应，比如查阅的介电参数对应的频点是3 GHz，而系统工作频点是6 GHz，则要考虑查阅的参数是否适用。对于超宽带系统而言，则更是需要注意介电参数对频率的依赖特性。更详细的讨论可参考相关电介质物理的理论。

尽管有一些理论可以用来预测材料介电参数，但更为可靠的方法是直接测量材料的介电参数。材料复介电常数的测量理论与技术已经发展和应用了数十年，尽管已经有了非常成熟的技术和产品，但是这个领域的研究仍是一个重要的课题。一方面，新应用催生的新材料研发对介电参数测量技术提出了越来越高的要求；另一方面，特殊场景（比如高低温）下的测量需求迫切需要开发复杂测量系统或者低成本、便携式测量系统。

总体上而言，材料复介电常数的测量技术可以分为2大类：谐振法和非谐振法。前者又可以包括2类方法——谐振器法和谐振器微扰法，后者则可以分为反射法、反射/传输法。进一步地，每一类方法又可以采用多种测量夹具，比如非谐振法常用的夹具有同轴线、波导以及喇叭天线等（自由空间法），谐振法常用的夹具有空气介质金属谐振腔、介质谐振腔等。各种测量方法/夹具在适用的频率范围、测量精度、对待测样品形状尺寸的要求等方面均存在差异，需要依据具体应用场景、测量成本等因素综合考虑。

同轴线反射法是非谐振法的代表性方法之一，其成熟产品已经获得了广泛运用。一种较为常用的测量方法及其理论模型（电容模型）如下图所示（参见《微波电子学——材料电磁参数的表征与微波测量技术》）：

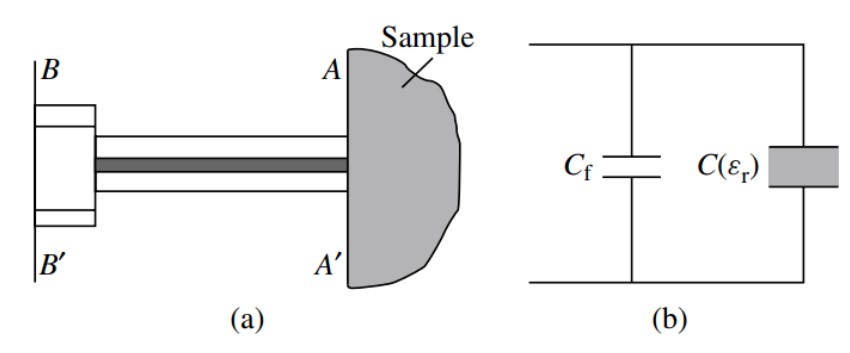
这里，假设待测样品为半无限大且与终端开路同轴探针接触，如上图a所示；对应的理论模型如图b所示：总电容由和并联构成，与样品介电性能无关，与样品介电性能有关。在平面测得的复反射系数可以表示为：

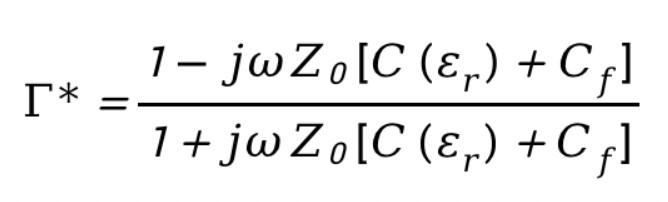
其中，分别包含角频率、同轴线特征阻抗、同轴线端接空气时的电容。经过对上式进行数学变换，可以得到复介电常数的表达式：

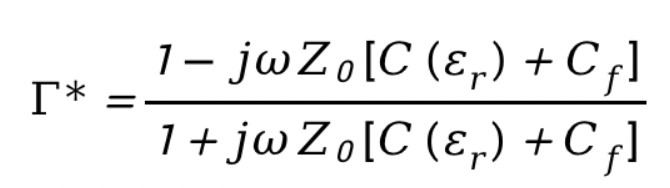
可以通过测量标准样品获得两个电容系数，比如去离子水（也可以是其它材料）。注意，分别对复反射系数的实部和虚部求解方程即可获得系数和。因此，只需要一个校准样品。测得标准样品的反射系数后，可以采用下式计算两个电容系数（Ref.: microwave electronics measurement and materials characterization）：

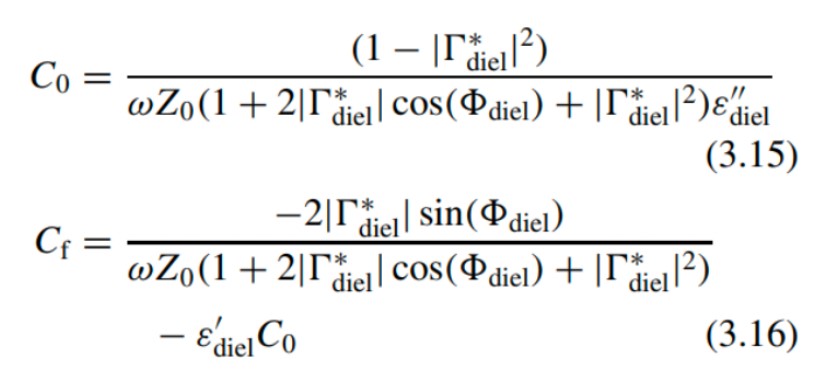
其中，还包含标准样品的复介电常数的实部和虚部。

下面以CST仿真实验来介绍同轴反射法测量介电特性的具体实施方法。首先，设计特征阻抗为50Ω的空气介质同轴传输线，设计结果——内导体直径3mm、外导体内径7mm，传输线长度理论上不影响特征阻抗，这里任意选取为20mm。仿真中，忽略同轴线导体损耗（亦即设置为PEC材料）。待测介质样品设置为立方体，同轴线端接待测介质样品，整体仿真模型如下图所示。

在待测样品相对介电常数为2、损耗正切为0.01时（需要留意，在CST仿真中，定义材料损耗正切时，如何考虑色散效应有多种选择；此处，损耗正切定义频点为0 GHz、色散模型为Debye模型、拟合阶数为自动设置亦即采用了“Const. fit - automatic”选项），拟合得到的材料介电特性如下（Eps’是实部、Eps’’是虚部、Eps TanD是损耗正切）。在1.5 GHz处（下文将以此频点为例，展示介电特性测量过程），拟合得到的材料相对介电常数为2、损耗正切为0.01，与设定值吻合。

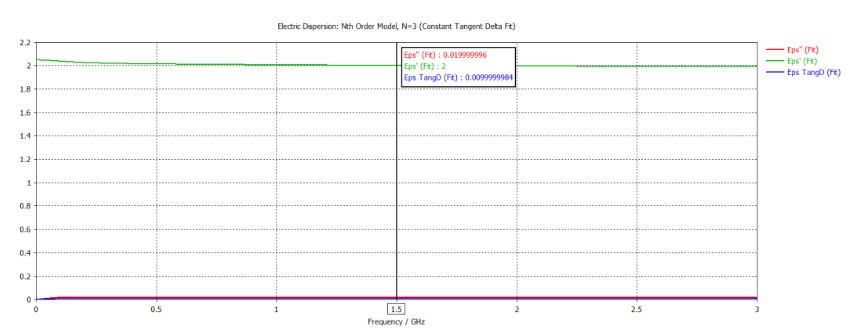
观察了样品大小对同轴线S11幅度的影响，所得结果如下图（样品边长取50、100、200mm，对应S11编号依次为3、4、5）：可以看到当样品边长达到100mm时，可以近似认为满足“半无限大”的假设。

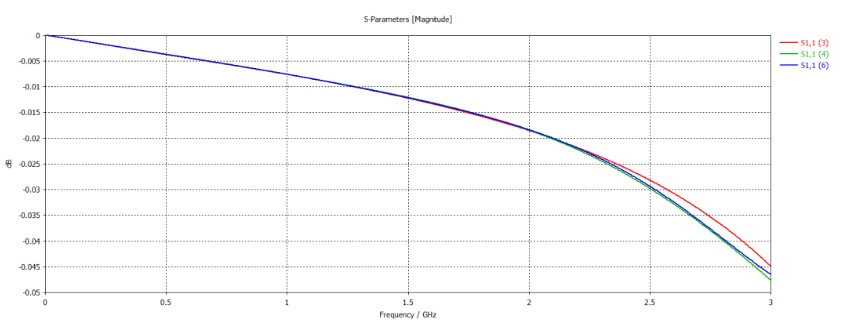
下图是样品大小对S11相位的影响结果：

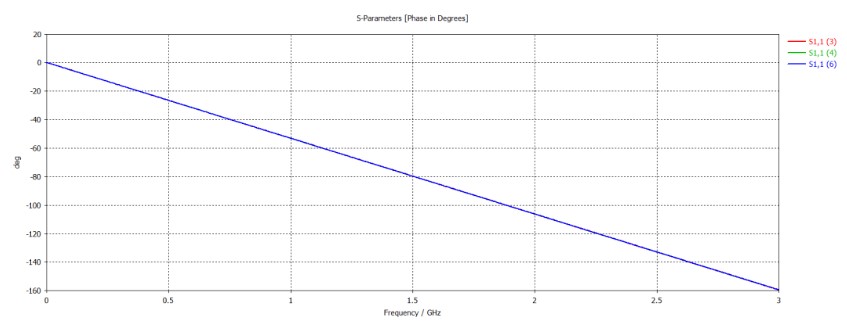
通过上面的仿真，确定待测样品边长为100mm。从CST仿真结果中将S11的幅度和相位数据导出，然后换算为复反射系数，进而得到反射系数的幅度和相位；同时，需要将标准样品的相对介电常数和损耗正切换算为复介电常数的实部虚部形式；至此，便可利用前述的(3.15)和(3.16)计算系数两个点电容系数。

S11的实部虚部形式如下：

导出的文本格式数据如下图所示（第一列为频率，第二三列为实部虚部）：

然后，依据复数的定义可以得到幅度和相位。

假设待测样品相对介电常数为2.5、损耗正切为0.02，拟合得到的材料参数如下：

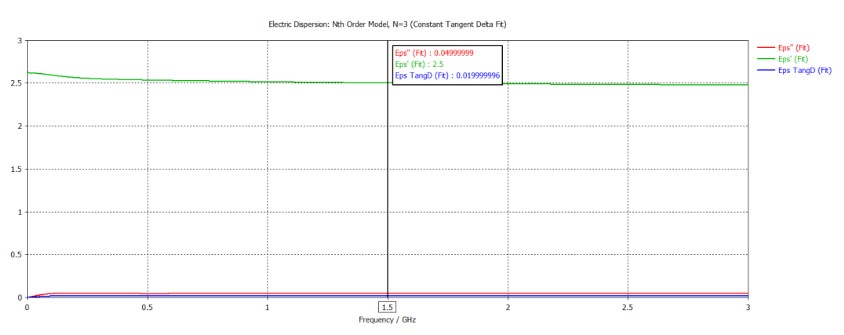
仿真得到其S11，如下图：

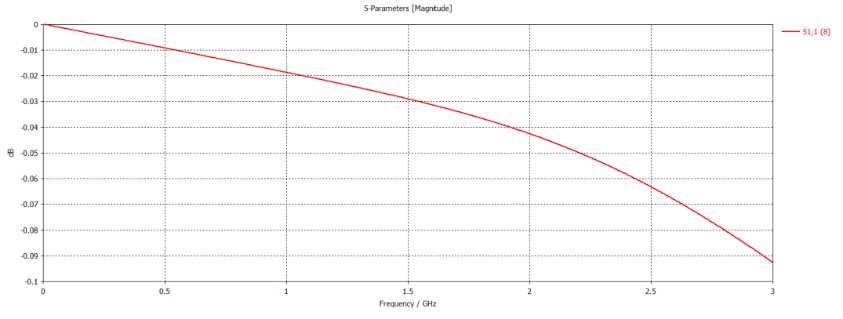
导出复数反射系数后，代入前述的复介电常数计算公式，得到提取出的复介电常数。这里，以1.5GHz频点为例进行展示。编写了如下的MATLAB程序，用于上述的校准和测试结果参数提取：

clc;clear;close all;

%% calibration

% input S11 of calibration sample

data01=[1.5000000000000 0.17837039618894 -0.98255058842766];

% frequency

freq=data01(:,1);

% reflection coefficient, equal to S11

Gamma_re=data01(:,2); % real part

Gamma_im=data01(:,3); % imaginary part

Gamma_mag=sqrt(Gamma_re.^2+Gamma_im.^2); % magnitude

Gamma_phase=phase(Gamma_re+1j.*Gamma_im); % phase

% real part of permittivity of calibration sample

ep_sample=2.0;

% loss tangent of calibration sample

loss_sample=0.01;

% imaginary part of permittivity of calibration sample

ep_im_sample=ep_sample*loss_sample;

% angular frequency

omega=2.*pi.*freq*1.5e9;

% characteristic impedance of coaxial line

Z0=50;

% eq.(3.15)

C0=(1-Gamma_mag.^2)./(omega.*Z0.*(1+2.*Gamma_mag.*cos(Gamma_phase)+Gamma_mag.^2).*ep_im_sample);

% eq.(3.16)

Cf=(-2.*Gamma_mag.*sin(Gamma_phase))./(omega.*Z0.*(1+2.*Gamma_mag.*cos(Gamma_phase)+Gamma_mag.^2))-ep_sample.*C0;

%% sample under test

% measured S11 of the sample under test

data02=[1.5000000000000 0.14643780930241 -0.98584447678300];

% frequency

freq02=data02(:,1);

% reflection coefficient, equal to S11 

Gamma_re02=data02(:,2); % real part

Gamma_im02=data02(:,3); % imaginery part

Gamma02=Gamma_re02+1j.*Gamma_im02; % complex form

% solve for complex permittivity of the sample under test

ep_complex_sample02=(1-Gamma02)./(1j.*omega.*Z0.*C0.*(1+Gamma02))-Cf./C0;

ep_sample02_re=real(ep_complex_sample02); % real part

ep_sample02_im=-imag(ep_complex_sample02); % imaginary part

loss_sample02=ep_sample02_im/ep_sample02_re; % loss tangent

上述MATLAB程序的主要工作过程如下：

1. 导入校准样品的S11亦即反射系数（这里是仿真得到）

2. 依据“实部-虚部”形式得到校准样品反射系数的幅度和相位

3. 利用校准样品材料参数等信息以及校准公式计算C0和Cf

4. 导入待测样品的S11（这里是仿真得到）

5. 依据待测材料复介电常数公式进行计算，得到其实部虚部及损耗正切

最终，MATLAB程序得到的待测样品相对介电常数为2.4681、损耗正切为0.02，与设定的材料参数吻合（相对介电常数设定值为2.5、损耗正切设定值为0.02）。相对介电常数误差为-1.3%。表明前述方法及程序是准确可靠的。

需要指出的是，同轴反射法还有其他模型，此处暂略；此外，由于待测样品表面可能凹凸不平，导致同轴探头与待测样品之间存有空气间隙，这可能引起测量误差。后续有机会再继续介绍。