写在前面

算是非常经典的网络了，它是由牛津大学计算机视觉组（Visual Geometry Group）和Google DeepMind公司的研究员一起研发的 “直筒型“ 的网络。既然在看这篇文章，想必已经对十分熟悉了。有一些特别明显的缺陷，如网络的参数量较多，模型检测准确率也不是很好，总之VGG网络效果不理想。之后的一段时间，人们总是将网络变得更宽更深（如GoogleNet、ResNet）,以期待达到更优异的效果。

事实上也是这样，更深更宽的网络更容易满足需求。这样，VGG变得鲜有问津。这时，一位大佬——丁霄汉，相信科学技术总是螺旋式的上升，捡起了VGG模型，给其注入了新思想，便横空出世。

首先我们先来解读一些的取名含义，Rep全称为re- parameterization（重参数化），Rep是指首先构造一系列结构（一般用于训练），并将其参数等价转换为另一组参数（一般用于推理），从而将这一系列结构等价转换为另一系列结构。估计这段话大家读的似懂非懂，对于来说，就是在训练阶段会训练一个多分支模型，然后利用重参数化将多分支模型等价转换为单路模型，最后在推理时使用单路模型。

为什么要这样做呢？因为在训练过程中往往多分支的结构会得到更高的性能收益，即在训练时采用多分支结构来提升网络性能，在推理时，将多分支结构转化为单路结构，这样会使推理速度大大加快！

RepVGG结构

听了上文的讲解，不知大家对RepVGG有了多少了解，还有很多疑惑是正常的，不要着急，下面会详细的对RepVGG的结构和设计进行分析RepVGG模型具有一个类似于VGG的拓扑结构，没有任何分支，模型只采用了3x3的卷积核和Relu激活函数。【注意：这里的RepVGG模型指的是推理（inference）时采用的结构，训练（training）时结构不是这样的】模型的结构如下图所示：

从上图我们可以看出，在RepVGG的训练阶段，其结构借鉴了ResNet，同时引入了残差结构和1x1的卷积分支，在论文中也证明了加入残差结构和1x1的卷积均可以提升网络的性能，如下图所示：

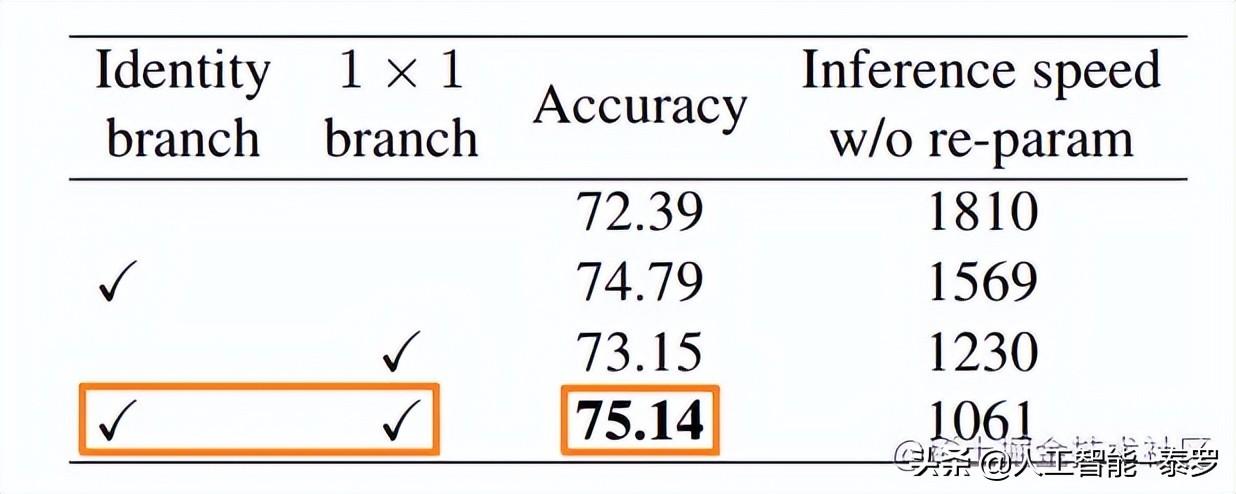
至于RepVGG的推理阶段，其结构就是简单的3x3卷积同Relu函数的结合。

多路模型转单路模型

这一部分绝对是RepVGG的核心了！！！re- parameterization（重参数化）要做的其实就是要将多路模型转成单路模型。首先我们要搞清楚我们要转换的对象，即多路模型指什么？单路模型指什么？这两个模型在上文已经提及，多路模型指的就是在训练阶段的模型，而单路模型指的是在推理阶段的模型，如下图：

现在我们的目标有了，即将上图右侧模型转换成左侧。仔细观察左右两图的区别，可以看出我们只需要将上图黄框部分进行转换就可以了。下面来看看作者是怎么进行转换的下图大致描述了多路模型转换成单路模型的过程，从①到②涉及到了将3x3卷积和BN层的合并、1x1卷积转换为3x3卷积及残差模块等效为特殊权重的卷积层。【注意：可能有小伙伴发现上文图中的卷积后都没有BN层，为什么这里有了了，其实一般卷积后都会跟上BN进行归一化，上图只是省略了网络的一些细节】

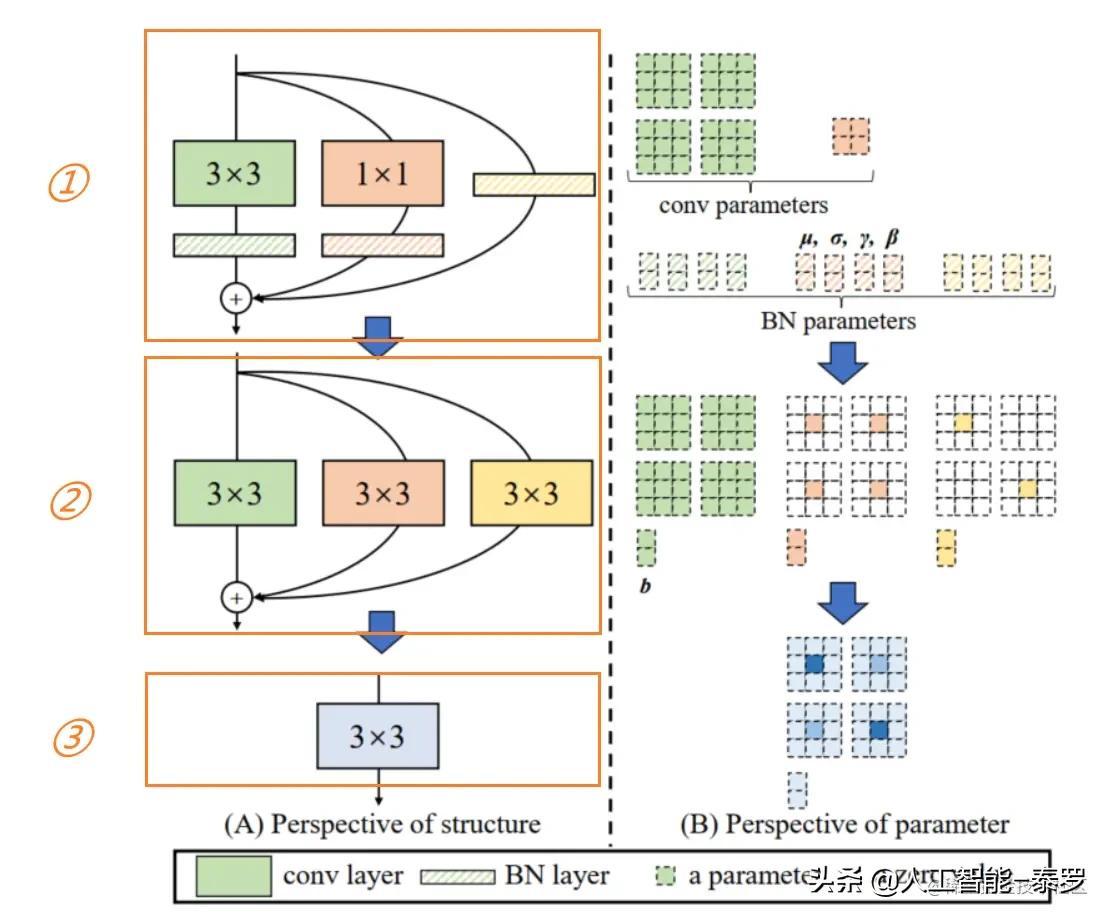
1、卷积层和BN层的合并

上图展示了卷积层和BN层合并的推导过程，非常容易理解。但需要注意的是这里的卷积层含有偏置b，往往现在带有BN结构的卷积都不含偏置b了，论文中的推导结构就没带偏置b，如下图所示：可以看出，下式和上图推导结构是一致的【符号表示有区别，没有偏置项b】

2、1x1卷积转换为3x3卷积

1x1卷积怎么转化为3x3的卷积呢？不知道大家有没有什么想法‍♂️‍♂️‍♂️我觉得这个大家应该是很容易就可以想到的——补两圈0！所以这部分其实是没什么好说的，论文中也是一笔带过。但这里我还是想提醒大家注意一下，因为我们的三路输出最后会通过Add操作，因此在使用3x3卷积时应该使用same形式，即保证输入输出的特征图维度不变

3、残差模块转换为3x3卷积

我们知道残差模块就是一个恒等映射，即要求输入等于输出。这一步该怎么实现呢？这里我们可以使用卷积核权重为1的1x1卷积，因为这样的卷积核不会改变输入特征图的值，这样我们就可以将残差模块等效为1x1的卷积操作了。之后再利用第2步将1x1的卷积转化成3x3的卷积。

卷积的可加性原理

完成了上述三步，我们就可以实现从①到②的变换，即现在我们得到了含3路3x3卷积的结构，接下来就是要实现从②到③的转化，即要将含3路3x3卷积的结构变换成只有1路3x3卷积的结构⛳⛳⛳这里需要利用卷积的可加性原理，即如果几个大小兼容的二维核在相同的输入上以相同的步幅操作以产生相同分辨率的输出，并且它们的输出被求和，我们可以将这些核在相应的位置相加，从而得到一个产生相同输出的等效核。这句话很好地总结了可加性原理，但是当我开始看到这句话的时候也是不明白为什么，后面也是自己画了一些图，就恍然大悟，所以我想说很多时候我们应该多动手，好脑子不如烂笔头下面给出整理的图片帮助大家理解，如下图：

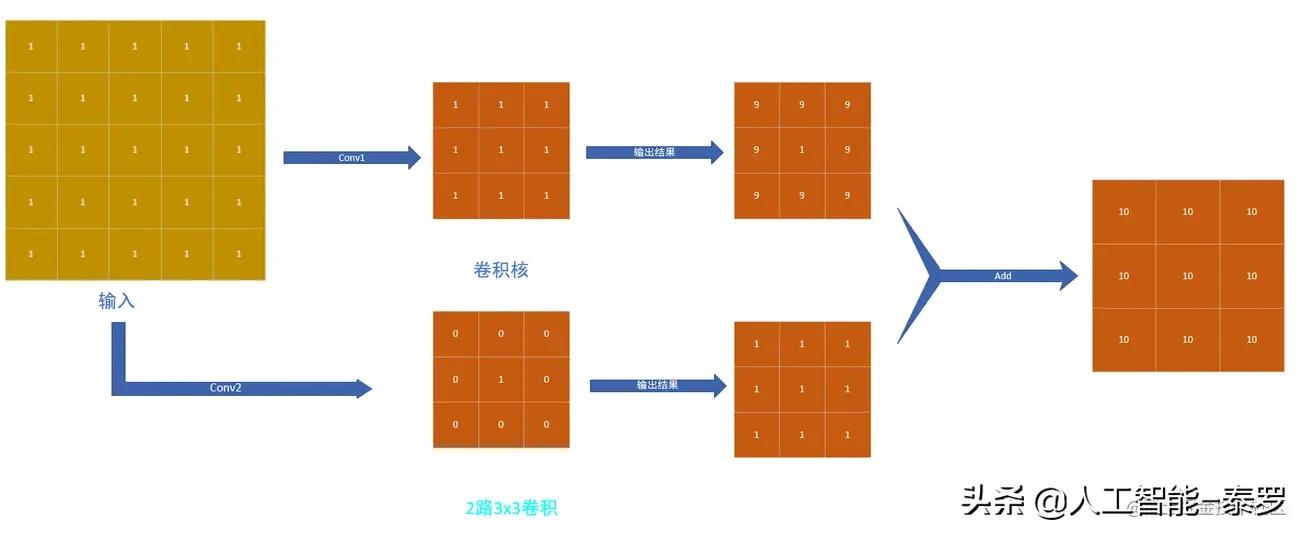
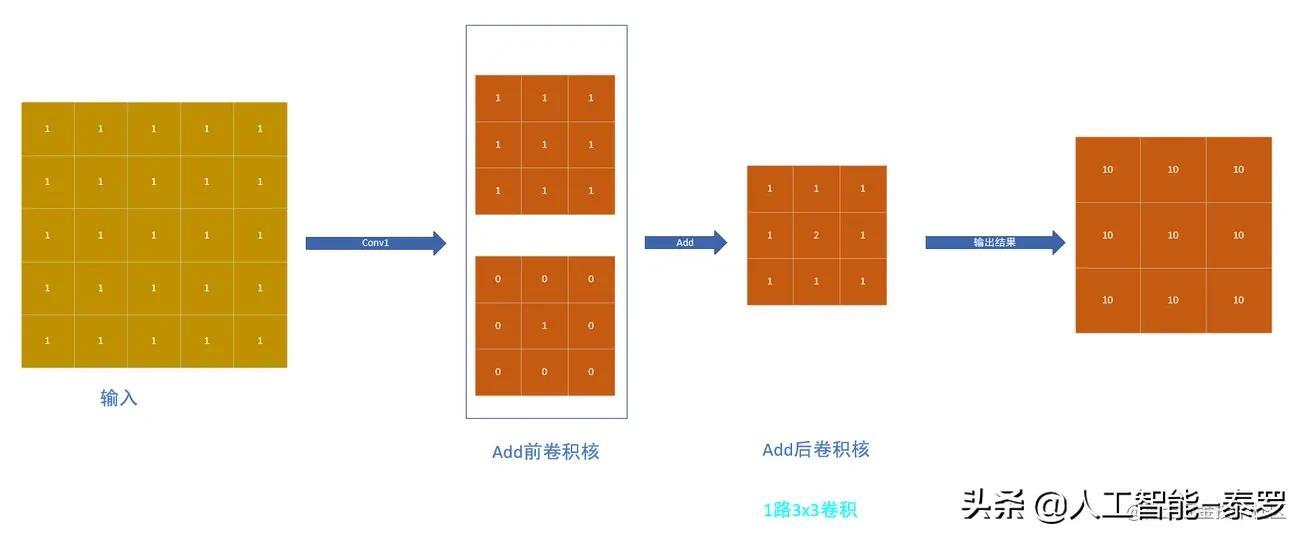
看了上图可以发现，不管我们是先进行卷积得到结果后再进行Add操作，还是先将卷积核的值先相加得到新的卷积核，然后再进行卷积，所得到的结果是一样的，这就是卷积的可加性。由此可知，我们将②变为③其实只需要将三个3x3的卷积核的值进行相加即可！

实验结果

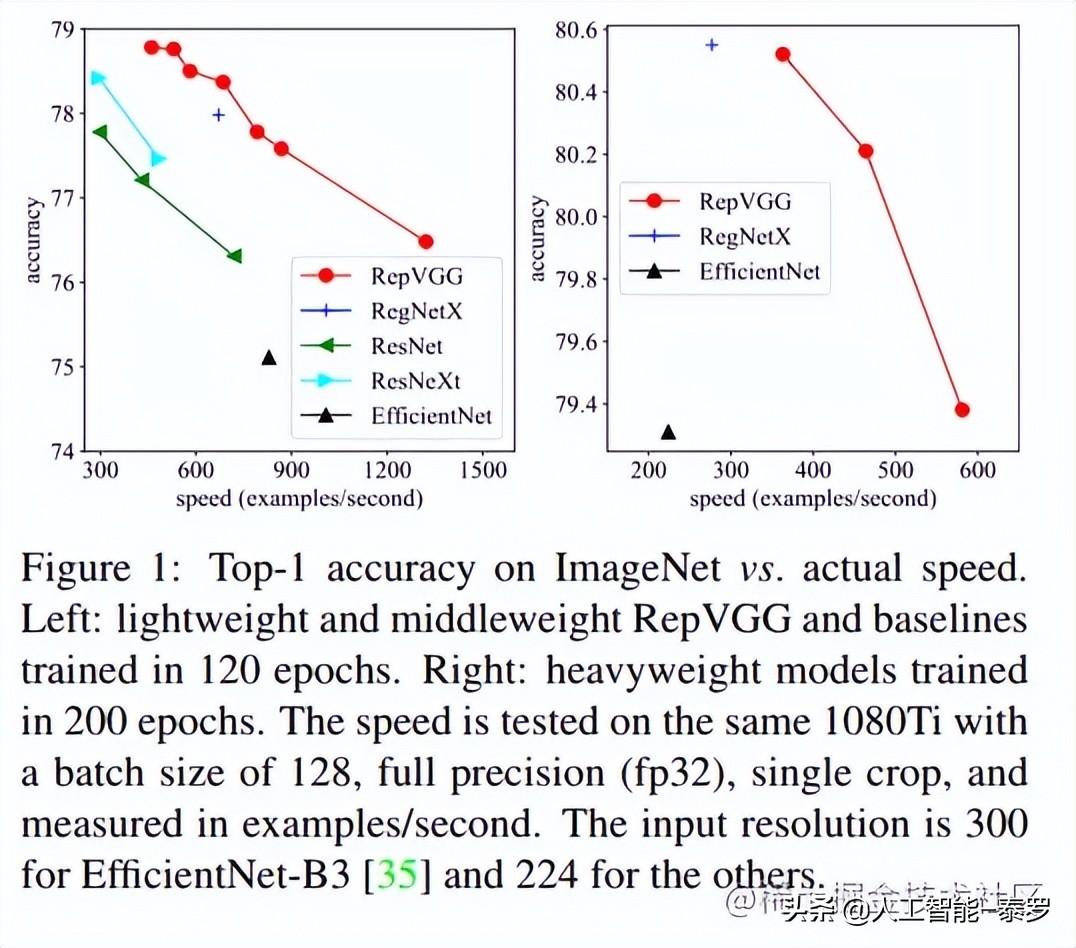
上面其实就把RepVGG最核心的给讲完了，下面来看一下RepVGG的效果叭。可以看出RepVGG的效果还是很好的，特别的表5中RepVGG-B2的FLOPs是EfficientNet-B3的10倍，但1080Ti上的速度是后者的2倍，这说明前者的计算密度是后者的20余倍。

希望本文章对你有所帮助！感谢支持！