技术咨询
代买器件
商务客服
研发客服对于 DAC 应用，希望来自 DAC 的噪声占主导地位，并且人们不希望仅仅为了确保传输的噪声频谱是白噪声而在链的后面添加噪声。
本文引用地址：在检查数据转换器的性能时，经常会看到图1所示的情况。
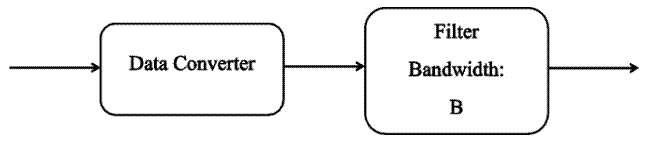
图 1. 数据转换器使用的简化框图
奈奎斯特带宽 (B N )中数据转换器输出的总噪声功率为 N。滤波器可以是带通或低通滤波器，带宽为 B o。通常，假设滤波器输出的噪声功率为：
滤波器输出的噪声功率 = N(B o / B N )
等式 1。 请注意，该等式对于任何中心频率下可能跟随 ADC 的任何合理滤波器都大致成立。“合理的过滤器”是指不太狭窄的过滤器。
公式 1 假设噪声是白噪声，或者随频率变化。
你的作者想知道；这个假设（通常称为伪[14]假设）在什么条件下成立？
参考文献[3]到[32]涵盖了这个问题的各个方面。为了澄清问题，作者还对具有各种输入的数据转换器进行了一些模拟。本系列了结果。
他只考虑均匀量化（所有步长相等），因为它通常用于高速数据转换器。此外，没有考虑西格玛-德尔塔转换器。
对于 ADC 应用，通常将 RF 链增益设置得足够大，以便来自先前组件的噪声比高 3 至 5 dB，因此频谱并不重要。然而，这可能会增加系统成本，因为需要更高的 RF 增益和 ADC 的更高动态范围。
对于 DAC 应用，希望来自 DAC 的噪声占主导地位，并且人们不希望仅仅为了确保传输的噪声频谱是白噪声而在链的后面添加噪声。
峰值、平均值和均方根值
定义输入信号的电平非常重要。图 2 显示了用 5 位量化的正弦波。该信号的电平通常称为0 dBFS；其中 FS 指量化器上的满量程。但是，射频工程师通常处理均方根值。由于正弦波的均方根值比峰值低 3 dB，因此图 2 的正弦波处于 -3 dBrmsFS 或 0 dBpeakFS。
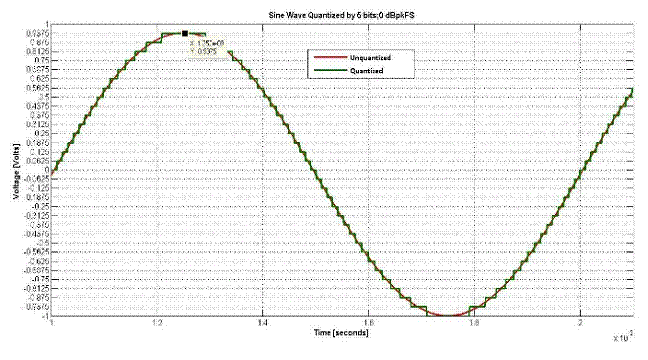
图 2.
对于本系列的其余部分，信号电平将以 dBrmsFS 或 dBpeakFS 为单位指定，
另请注意，由于功率是电压的平方，因此该恒定包络正弦波的峰均功率比 (PAPR) 为 3 dB。事实上，所有带通相位或调频恒定包络信号（例如 MSK）的 PAPR 均为 3 dB。
“等一下！” 你可能会说，亲爱的读者。“MSK 等恒定包络信号的 PAPR 不是 0 dB 吗？人们就是这么称呼它的。”
事实上，当人们以这种方式提到PAPR时，他们指的是包络的峰值功率与包络的平均功率的比率。特别是，在表征信号的复包络[33]时使用对 PAPR 的引用。由于我们关心的是该系列中的实际电压，因此 PAPR 将是实际峰值功率除以实际平均值功率。该 PAPR 将比通常引用的 PAPR 高 3 dB。在下一篇文章中，我们将继续讨论模数转换器 (ADC) 输出的频谱。
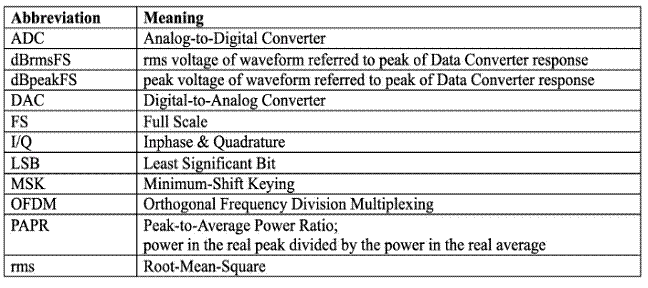
使用的缩写
请使用下表来了解本系列的其余部分。
相关文章
