0 引言

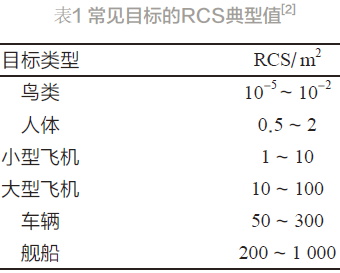
产品的开发中，测试和验证过程需要相应的目标作为工具，在开发阶段要开展大量的测试和实验，其中目标的截面积(Radar Cross Section, RCS) 值是衡量探测性能的重要指标，RCS 值与目标的形状、尺寸、结构及材料有关，也与入射电磁波的频率、极化方式和入射角等有关，实际目标的RCS 值，并不是一个确切的值，不同的姿态有不同的值，有些目标正面侧面RCS值可能相差甚至几百上千倍^[1]，表1 给出的是几种常见目标的RCS典型值。为了提取目标，目标的有效反射值一般定义为以某种极化的某个距离的平均RCS值。真实的目标有复杂的反射特性，关于在不同极化和频率下的有效反射值的测量，形成了一个既定的研究领域。

由于真实目标的RCS值的不确定性，在雷达的研究和探测性能的验证测量中，只能给定不同目标的典型值来作为衡量依据。

同时形成杂波的背景是静止的，杂波的多普勒值约为0，目标是运动的，其多普勒值相对于背景杂波突出，据此，可从杂波中提取出目标。

产品研发过程中以飞机舰船作为目标，成本高，也受空间飞行等多方面的限制，采用标准的反射器作为实验和测试的目标工具，可为开发活动提供方便、廉价的技术途径，同时的指标特性是可控、可计算的，基于此，可对雷达性能指标量化测试、分析提供支撑。本文针对雷达反射器的应用需求，描述了雷达反射器的原理，指标相关参数，以及设计计算方法和工程常用的基本构型。

1 功能介绍

雷达反射器是一种被动装置，将入射的电磁能量直接反射回能量源。雷达基本原理是利用偶镜原理，由两个或3 个交叉安装的导电平面相互垂直组装在一起，形成偶镜，入射线在其平面多次反射后，形成与入射线相平行的回波。相互垂直的面，具有极高的反射率，因此即使是较小尺寸的反射器也会产生足够强的回波^[3]。

雷达类型按面板形状分有方形、三角形、扇形；按结构形式分有固定式、可拆卸式、混合式；按面板个数分有两面反射器、三面反射器实际应用中，反射器的安装总是有机械误差的，不可能保证反射器与入射线的绝对垂直，三面的反射器可保证一定角度范围入射信号多次反射，在空间形成与入射平行的反射信号，所以在实际使用中，一般采用三面角反射器。

三面角反射器是一种典型的雷达反射器，经常用于校准或测量雷达系统的性能。在使用中它有以下一些有利的特性：

1）可产生远大于其物理尺寸的RCS 值；

2）大角度范围的信号反射；

3）角度容差大，场景容易布置；

4）RCS 值确定，容易计算。

同时也有以下不利的特性

1）理论计算RCS 值是基于自由空间中的，与周围的环境反射体( 如地面) 无关；

2）射线入射角与反射面平行时，RCS下降相当显著；

3）如果一个反射面向前倾斜，使其最大RCS 方向相对于地面处于一个浅掠角，那么地面波瓣就会出现问题，降低RCS 计算的准确性；

4）如果反射器被放置的底板与地面平行，那么反射器的RCS 值严重减少。

2 相关要素分析

2.1 反射指标定义

雷达目标反射信号的指标用(Radar Cross Section, RCS) 度量，目标的RCS 取决于目标结构（形状和材料）、雷达工作频率、雷达极化方式和雷达观测角^[3]。

RCS定义是基于各向同性反射体的投影面积来表示。即RCS 值为1 m2 的反射是一个直径约为1.13 m 的球形导体，在垂直于信号入射方向投影面积为1 m² 的等效反射。

从RCS定义来看，由于只有中间的一个小区域，能准确地反射雷达方向的入射能量，形成回波，其他区域的入射信号被反射到空间其他方向，目标的投影只有很小的区域是有效的，如图1 所示。因此，能够定向反射入射信号的反射器只需要很小的几何尺寸就可以有几平方米的RCS 值^[4]。

图1 反射示意图

根据雷达角反射器定义和原理，设计时须考虑以下3个方面因素：

1）目标可视面积

2）雷达信号入射角

3）可能形成的频率和尺寸

2.2 可视面积分析

首先以1 个相互垂直的二面反射器入手做简化分析。如果角反射器的边长实质上大于波长，则可根据几何光学定律计算投影面积。

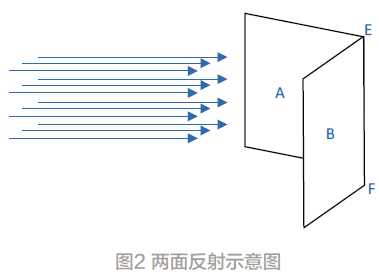
两个面的情况时，需要入射线与反射面的棱EF 相垂直，才能形成回波，可视面积等于面AB 在射线垂直方向的投影面积，如图2所示。当AB 面与入射线夹角为45°时，投影面积最大，此时计算公式为：

式中：A_PROJ：投影面积；A_WR：反射面实体面积

根据自由空间损失可计算得出RCS值σ ，计算公式为：

式中：A：镜面反射面积；λ ：雷达波长

综合式（1）（2），可得到二面反射器的RCS最大值σ ，计算公式见式（3）：

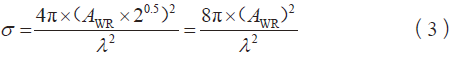
2.3 入射角分析

当反射面与入射角度不等于45°时，部分射线只有1次反射，不能形成有效回波，部分射线有2次反射，形成有效回波，所以有效反射面是小于投影面积的，有效反射面积与投影面积关系如图3所示。射线a经2次反射形成有效回波，射线b 只有1 次反射，不能形成有效回波，AB为投影面积，AC为有效反射面积。

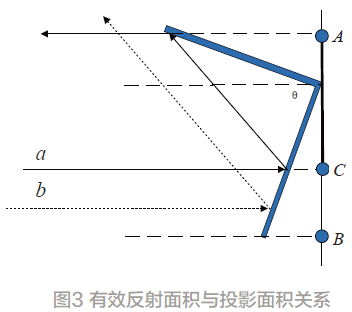
根据几何关系，可计算反射面与入射线夹角0°<θ<90°时，有效反射面积A_eff的值为：

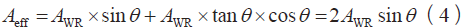
RCS值σ为：

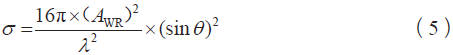
2.4 影响

金属表面对电磁波的作用就像镜子一样，这只是一种简化概念，实际上的反射过程是金属表面吸收能量，自我振荡并再次辐射能量，不同区域的射线反射有不同的路程差，不同的路程差造成不同的相位差，因此当入射角不同时，回波会与入射波相叠加造成不同的影响。

与箔条类似，反射表面可以与波长发生共振，反射面必须至少是偏振方向波长的一半，但是必须两个反射面，即角反射器的最小长度是一个完整波长。射线通过完整波长角反射器中的共振，最大可以测量到RCS的4倍。反射器受到谐波的影响，有谐振的增益，也有衰减的情况，在一半波长（1.5 λ ，2.5 λ …）的奇数倍下，RCS 值减少，当反射器尺寸大于波长10倍以上时，影响可以忽略^[5]。

2.5 机械安装精度影响

上述分析是基于每个相邻面板夹角严格为90° 的情况下的结果，实际的加工制造必然有公差，非常细小的公差也会影响反射器的实际效果。使用损坏、装配误差、加工精度都可能使夹角不是严格的90° ，实际使用中，也不可能要求其绝对符合理论值，但需要掌握误差与反射效果之间的变化关系，以保证反射器的实际反射效果满足应用的需求即可。

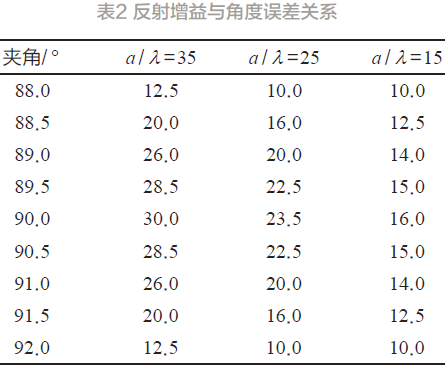
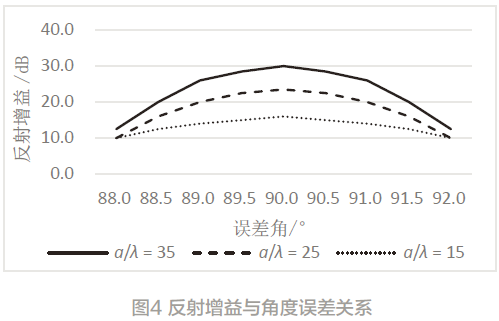
在边长a 与波长λ 比在35、25、15 时，不同夹角误差时所的反射增益值^[6]见表2 与图4 所示。

3 三面角反射器应用

实际应用中，反射器的安装总是有机械误差的，不可能保证反射器与入射线的绝对垂直，三面的反射器可保证一定角度范围入射信号3次反射，在空间形成与入射平行的反射信号，所以在实际使用中，一般采用三面角反射器。

3.1 方形三面角反射器

角反射器反射面由3 块方形面板组成，每个面板以相对90° 角安装在一起，如图5 所示，因此，几何投影面积由3 个分区组成，每个分区由式（1）计算得出，射线经3 次反射，可得出适用于方形三面角反射器的RCS值计算公式，见式（6）。

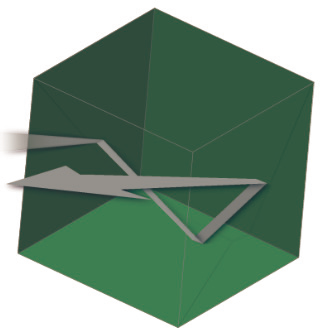
图5 方形三面角反射器

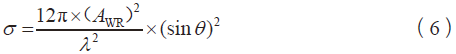
3.2 三角形三面角反射器

具有3个正方形面的角反射器在机械上相对不稳定，因此，大多数情况下，部分表面被简化为三角形面，如图6所示，有效反射面减小，但结构具有较大角度范围的反射波束宽度，该三角形角反射器的有效雷达横截面计算公式为^[5]：

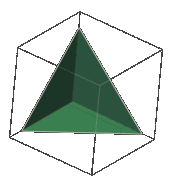
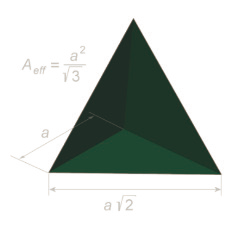
图6 三角形三面角反射器

式中：a：三角反射面棱长；λ ：雷达波长

类似天线-3 dB 波束宽度的概念，这种角反射器-3 dB 反射增益的角度范围为40° ，因此，8 个这样的角反射器所构成立方体，如图7 所示，可实现全方位的有效反射^[7]。

该角反射器由12 个等腰三角形拼接而成，在实际施工中，使用3 块尺寸相等的方形板，开槽，镶嵌焊接在一起。这种结构的角反射器的RCS 值可实现大于反射器机械尺寸500 倍的值^[8]，采用这种反射器，可更方便地在实验使用和定量测试。

参考文献：

[1] GEORGE T. RUCK. Radar cross section handbook[M].Los Altos,Coalifornia,2002.

[2] SEVGI L, RAFIQ Z, MAJID I. Radar cross section(RCS) measurements[J]. IEEE antennas and propagation magazine,2013,55(6):278-291.

[3] 牛瑞,陈刚, 刘志铭,等.雷达角反射器的设计及应用[J].测绘科学与工程,2014,34(1):32-36.

[4] Christ ian Wolff. Corner reflectors[EB/OL]. 2022, https://www.radartutorial.eu/17.bauteile/bt47.en.html.

[5] LUZI G, BARRA A, GAO Q, et al. A low-cost active reflector and a passive corner reflector network for assisting landslide monitoring using multi-temporal InSAR[J].Remote Sensing Letters,2022,13(11):1080-1089.

[6] 闫华,李胜, 殷红成.非等边三面角反射器RCS的解析表达与有效散射区域分析[J].中国传媒大学学报(自然科学版),2019,26(1):5-14.

[7] TOLEDO F, DELANOE J, HAEFFELIN M, et al. Absolute calibration method for frequency-modulated continuous wave (FMCW) cloud radars based on corner reflectors[J]. Atmospheric Measurement Techniques,2020,13(12):6853-6875.

[8] MODI A Y, ALYAHYA M A, BALANIS C A, et al. Meta surface-based method for broadband RCS reduction of dihedral corner reflectors with multiple bounces[J]. IEEE Transactions on Antennas and Propagation,2020,68(3):1436-1447.

（本文来源于《电子产品世界》杂志2023年3月期）