实验要求

在第一次作业中的第二小题，练习了根据信号的波形写出对应信号的表达式。但在实际中，我们观测到的信号往往是在示波器上的波形，此时该如何获得这些波形的数学表达式？

测量波形的示波器

本质上讲，实际信号中都会带有随机性，是没有确定的数学表达式的。但在某些情况下，我们是预先知道信号的类型的，比如正弦波，但不知道信号的一些参数。例如幅值、频率和相位。如果这些参数知道了，便可以写出对应的信号数学表达式了。在这种情况下，从观测到的带有噪声的信号波形中回复处信号，则属于信号参数估计的内容了。

部分电子元器件

在实际应用中，信号的参数往往非常重要。下面举一个例子：如果手边只有一个万用表，但没有能够测量电容、电感的RCL桥，为了想知道一个电容器件的准确容值，可以将待测的电容与一个电阻串联在一起。电阻的阻值可以使用万用表精确测量。使用一个信号源产生一个正弦波信号施加在RC串联电路上，使用示波器同时测量信号源的信号以及RC分压后的信号。

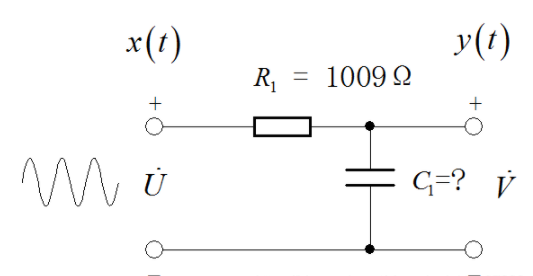
利用RC测量电子器件参数电路

根据电路原理，可以知道上述电路稳态输入输出正弦信号之间的关系如下：

V ˙ = 1 j 2 π f C 1 R 1 + 1 j 2 π f C 1 U ˙ = 1 1 + j 2 π f R 1 C 1 U ˙ dot V = {{{1 over {j2pi fC_1 }}} over {R_1 + {1 over {j2pi fC_1 }}}}dot U = {1 over {1 + j2pi fR_1 C_1 }}dot UV˙=R1+j2πfC11j2πfC11U˙=1+j2πfR1C11U˙

实测测量电路和示波器

因此，输入输出正弦信号的幅度之比为：
α = ∣ V ˙ ∣ ∣ U ˙ ∣ = 1 1 + ( 2 π f R C ) 2 alpha = {{left| {dot V} right|} over {left| {dot U} right|}} = {1 over {sqrt {1 + left( {2pi fRC} right)^2 } }}α=∣∣∣U˙∣∣∣∣∣∣V˙∣∣∣=1+(2πfRC)21

输入输出正弦信号的相位差为：θ thetaθtan ⁡ ( θ ) = 2 π f ⋅ R C tan left( theta right) = 2pi f cdot RCtan(θ)=2πf⋅RC

所以，只要能够测量出U，V两个正弦信号的幅度或者相位，频率，再加上已知电阻阻值R1.，便可以计算出来待测电容的容值。
C = tan ⁡ θ 2 π f ⋅ R = 1 − α 2 α ⋅ 1 2 π f ⋅ R C = {{tan theta } over {2pi f cdot R}} = {{sqrt {1 - alpha ^2 } } over alpha } cdot {1 over {2pi f cdot R}}C=2πf⋅Rtanθ=α1−α2⋅2πf⋅R1

已知上面的串联电路中的电阻nR1.=1009欧姆。示波器显示波形的数值可以通过已经存储在CH12.MAT中，数值的采样时间间隔fs=10微妙。

示波器采集的数值波形

请根据以上分析，求出待测电容nC1.的容值是多少。

提示：

在MATLAB中通过load()命令读取CH12.MAT中的数据；

ch12(:,1) 是V的数据， ch12(:,2)是U的数据。

使用MATLAB中fit命令来估计数据中的参数。
f = fit(x,y,‘fourier1’)

上面fit命令输出 f(x)=a0+a1cos(xw)+b1sin(xw)
中的a0,a1,b1,w等参数。

使用MATLAB计算出现的问题

使用MATLAB计算步骤

调入数据并绘制波形图

load ch12' t = linspace(0, 1400*10e-6,1400)' plot(t,ch12(:,1), t, ch12(:, 2))'

两个测量数据通道的波形图

（2）使用MATLAB 计算正弦波形参数

f1 = fit(t, ch12(:,1), 'fourier1')' f2 = fit(t, ch12(:,2), 'fourier1') f1: a0:119.1442, a1:-1.6132, b1:27.3382, omiga:2481 f2: a0:150.0722, a1:64.1255, b1:43.5524, omiga:2481

2. 使用MATLAB计算出现的问题

使用上述参数利用两个公式计算，会出现1.5倍的差异。tan ⁡ ( θ ) = 1.677 ,      1 − α 2 α = 2.6480 tan left( theta right) = 1.677,,,,,{{sqrt {1 - alpha ^2 } } over alpha } = 2.6480tan(θ)=1.677,α1−α2=2.6480

相关的矢量方差如下图所示：

MATLAB计算出的参数的问题

从MATLAB通过剪切板得到数据

首先在MATLAB命令窗口使用如下命令将CH12数据拷贝到WINDOWS剪切板。

cc(ch12)

然后通过下面的PYTHON程序将剪切板上的数据转换成两个数组，分别对应的输出和输入信号的采集的数据。

pastestr = clipboard.paste().strip('[').strip(']').split(';') data1=[] data2=[] for s in pastestr: ss = s.split(' ') data1.append(int(ss[0])) data2.append(int(ss[1])) plt.plot(data1) plt.plot(data2) tspsave('CH12', ch1=data1, ch2=data2) printf('a') plt.show()

进行函数拟合和参数计算

两个通道正弦波及其FIT曲线

根据的PYTHON程序重新计算输入和输出相应的数据对应的正弦参数，数据如下，所得到的估计参数与MATLAB相同。