虽然在工程中基本都是用SVPWM或其变形，很少用到SPWM，但是说到SVPWM优点的时候，总是将之与SPWM做对比，因此有必要对SPWM做一些了解。

本篇主要就SPWM的几点结论进行解释。

pwm

陈伯时著作中的一段话

想要理解这段话中的前半段背后的理论，首先需要理解两个概念。

电压利用率：逆变电路输出的线电压的基波幅值和直流母线电压Ud的比值。

因为母线端的电压有限制，为了输出更大的线电压，当然也就希望电压利用率越高越好了。

调制度：逆变器输出的相电压基波幅值与SPWM在线性调制区输出的最大相电压幅值（1/2*Ud）的比值。

调制度如果大于1，则进入过调制区域，本文仅考虑线性区域，即调制度不大于1的情况。

在谈SPWM或SVPWM的时候，首先需要明确我们的需求是什么？

为了让永磁同步电机朝一个方向匀速旋转，电机的定子需要产生一个匀速旋转的磁场，去牵引电机的转子。为了产生旋转磁场，要求电机UVW三相（空间相差120度）需要加载幅值相等，且在时间上相差120度相位的正弦电流。而为了产生这样的电流波形，需要在UVW三相上加载幅值相等，时间上相差120度相位的电压波形。如何产生这样的电压波形呢？

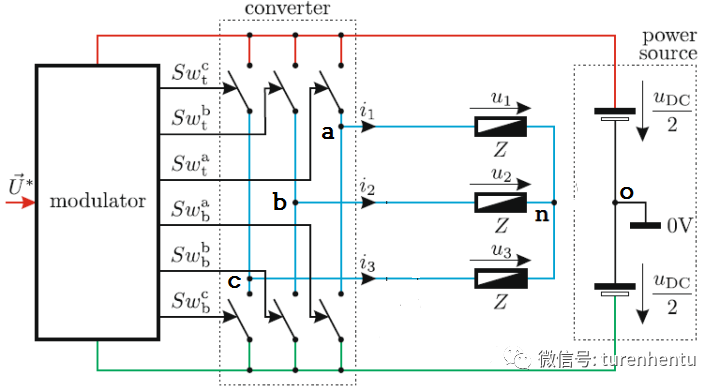
Fig1 电源中点为参考电位0

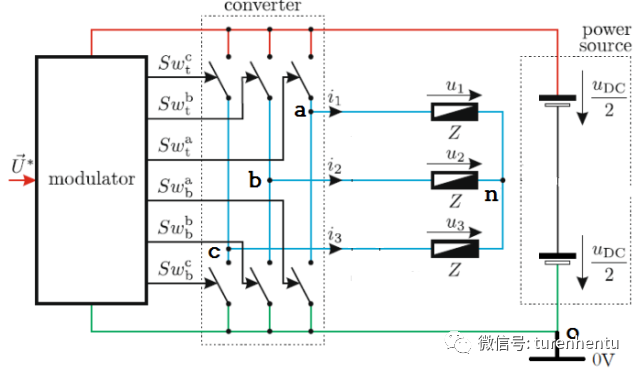
Fig2 电源负极为参考电位0V

1，SPWM的星结点电位是固定的。

为什么呢？这里需要说明的是，应该说星结点处，将实际脉冲等效后的电位为固定，此处电位并非每时每刻都为固定。因为动态分析下，星结点电位是波动的。如采用Fig1所示的参考电位选择方式，那么星结点n电位可能为1/6Udc，-1/6Udc，-1/2Udc（000）和1/2Udc（111）四种情况，如采用Fig2所示参考电位选取方式，那么星结点n电位可能为2/3Udc，1/3Udc，0 （000）和Udc（111） 四种情况。

具体分析不再赘述，考虑八种开关情况（100，101，110，011，010，001，000，111）即可。

基于上面的结论，有没有发现什么规律？

Fig2中的星结点电位似乎比Fig1中的高1/2Udc？

的确如此。

Fig1经常会出现在论文和书本教材中。

基于Fig1，若取三相参考电压（对地的端电压）为：

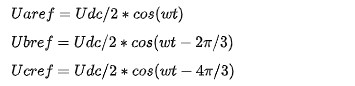
三相波形为：

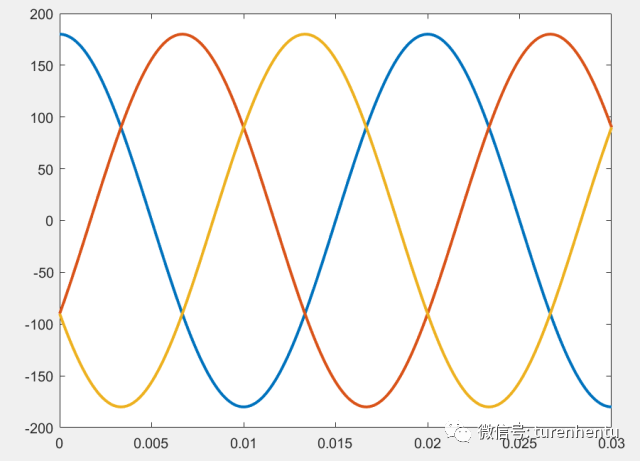
参考电位在电源中心，Udc=360V

则通过SPWM，即可获得最大的相电压幅值Udc/2。此时星结点电压恰好等效为0V。

Fig2才是实际使用中会出现的情况。

基于Fig2，取三相参考电压（对地的端电压）为：

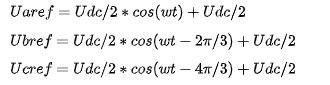
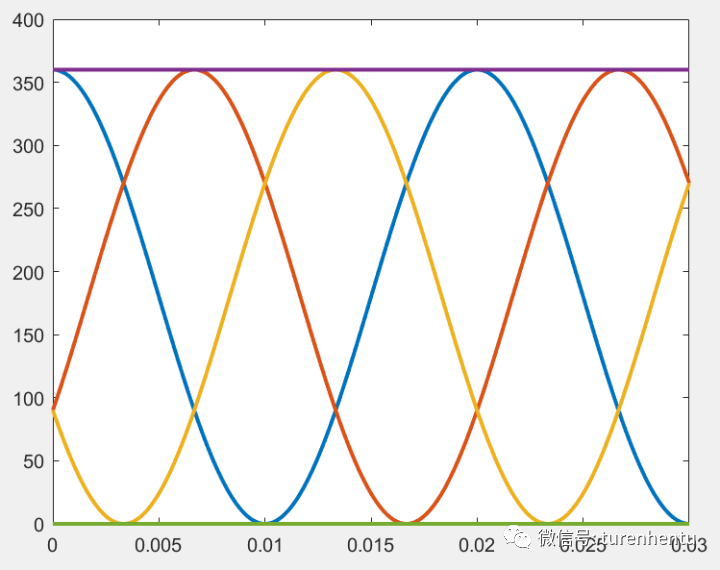
三相波形为

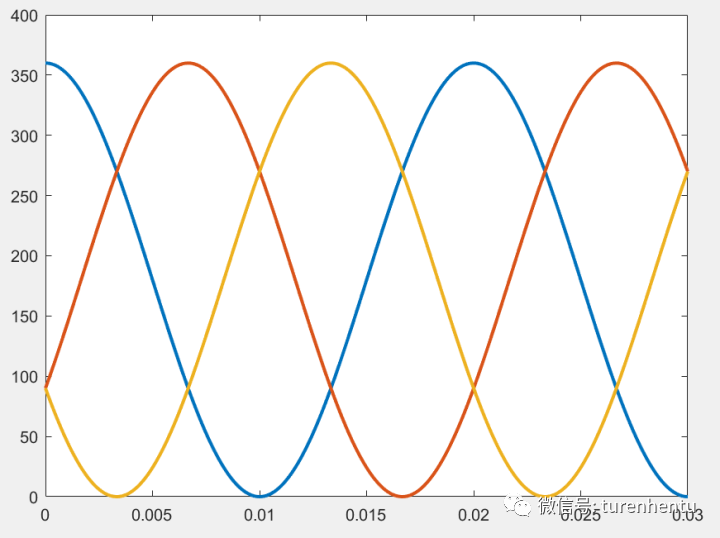
参考电位在电源负极，Udc=360V

则可通过SPWM获得最大相电压幅值Udc/2，此时星结点电压等效为Udc/2。

1.1，理论计算

假设SPWM的调制波电压（对地电压）为：

当B=0时，A=Udc/2，对应Fig1中的情况，此时星结点电压为0V；当B=A=Udc/2时，对应Fig2中的情况，此时星结点电压为Udc/2。

因此，SPWM调制方式下，参考电位确定后，星结点电位应是固定不变的。

1.2，仿真分析

假设Udc=360V，将调制度设置为1。分别对Fig1和Fig2的情况进行分析，可知无论是Fig1还是Fig2，其相电压仿真结果均约为180V，见Fig3，即参考电位的选取不影响相电压大小。

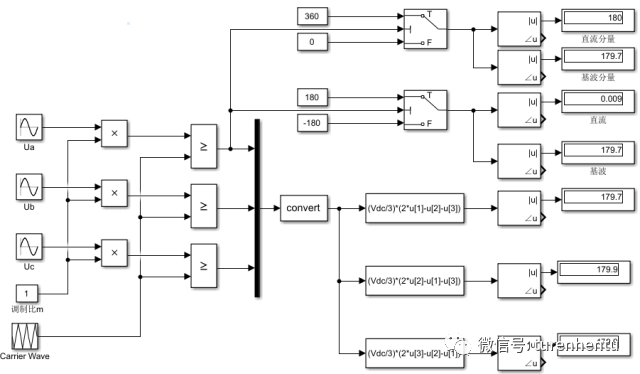
Fig3 相电压及端电压仿真

由下图仿真结果可知，无论是Fig1 还是Fig2中选择参考电位的方式 ，其星结点的电压基波分量均为0，采用Fig1 选取参考电位的方式，星结点等效电位为0V，采用Fig2选取参考电位的方式，星结点等效电位为180V，与理论分析相符合。Fig3中同样显示了a相的端电压的仿真结果。

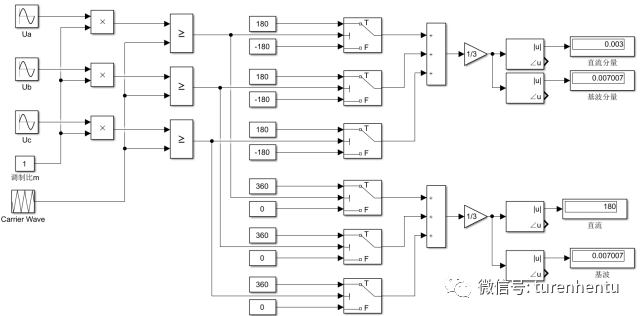
星结点电压仿真

2，SPWM的相电压幅值最大为1/2UDc

陈伯时书中对SPWM的定义

首先要注意限制条件。

第一，spwm三相调制波一定要是正弦波。

如果调制波是马鞍波那就是svpwm了，不属于spwm。

如果调制波是方波，梯形波或者三角波，也不能认为是spwm。

第二，为了保证不进入过调制区域，调制波幅值不能大于直流母线电压的一半。

即正弦波峰峰值要求不大于Udc。那么调制波的幅值最大值也就只能是Udc/2，因此线电压基波幅值为Udc/2*sqrt(3)。

根据电压利用率定义，可得SPWM的电压利用率最大值为Udc/2*sqrt(3)/Udc，即约为0.866。