设计是一项具有挑战性的任务，涉及线性度、效率、增益和输出功率之间的权衡。在这里，我们研究共发射极电路如何能够或不能用作。

本系列之前的文章讨论了小信号放大器，它通常设计用于增益和线性，而不是功率传输。如果接下来的电路具有纯电容输入阻抗，则小信号放大器可能会提供特定的电压或电流增益，而不会向实际负载传输任何明显的功率。由于小信号放大器不处理高功率电平，因此功率处理能力和功率效率也不是其主要设计要求。

在接下来的几篇文章中，我们将讨论一些截然不同的内容：射频。（PA）出现在发射机的输出端，负责将射频功率传输到天线。我们可以预计功率放大器的峰值交流电流在200毫安或更高的范围内——当然不是小信号。

这让我们区分了功率放大器和线性小信号放大器的重要区别。功率放大器的交流电流通常与其静态偏置电流相当。由于功率放大器处理大量的交流电流，而大偏置电流意味着线性操作较差，因此我们可以预期功率放大器基本上是非线性的。即使是A类功率放大器——最线性的功率放大器类型，也是本文的主要主题——通常被设计为提供等于晶体管偏置电流的峰值交流电流。

我们将通过检查功率效率和功率处理能力的问题来开始我们对A类功率放大器的研究，这两者在PA设计中都是最重要的。然后我们将看看我们是否可以通过使用共发射极级作为功率放大器来解决这些问题。在我们完成一些计算后，我们将介绍电感负载的A类功率放大器。

功率效率和功率处理能力

由于它们旨在提供大量的输出功率，因此功率放大器是射频收发器中最耗电的模块。例如，如果向天线提供30 kW功率的功率放大器效率仅为50%，则放大器本身将消耗30 kW。这可能是一个相当具有挑战性的热管理问题。

效率是一个主要问题，无论PA是向广播发射机的天线提供数十瓦的功率，还是向便携式通信设备的天线提供几瓦的功率。即使在低功耗的便携式应用中，低效率的PA在产生可用输出功率方面效率较低——事实上，PA会浪费电池提供的可用功率。使用更高效的PA，电池供电设备的使用时间可以更长。

另一个PA设计挑战来自大型信号功率放大器通常要处理的问题。考虑一个向50Ω天线提供1W射频功率的便携式设备。这需要提供20V的峰峰电压摆幅和200mA的峰值电流通过天线。正如你所看到的，即使在这种低功率应用中，晶体管也必须处理高压和电流水平，以在输出端提供所需数量的射频功率。

同时，在高功率应用中，有源器件必须处理远高于此的电压和电流。晶体管在它们可以处理的最大电压和电流水平方面以及在不损坏的情况下可以燃烧的最大功率方面都受到限制，因此这可能是有问题的。

我们可以使用共发射极放大器作为PA吗？

让我们研究一下使用共发射极（或共源极）级作为功率放大器的可能性。我们能否通过使用足够大的晶体管来有效地提供大量的输出功率？假设图1中所示的共发射极级向50Ω负载电阻（RL）提供1W的功率。

共发射极级电路图。

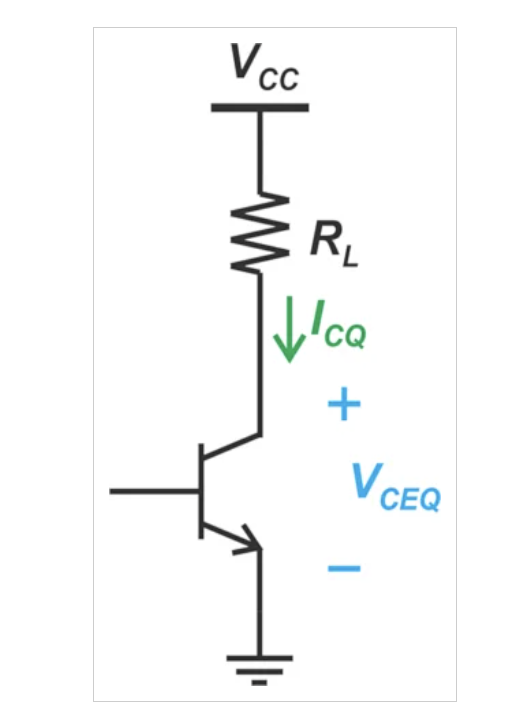
图1.共发射极放大器。

为了将图1中的电路用作PA，我们显然需要使用能够耗散几瓦到几十瓦而不被损坏的功率晶体管。然而，首要问题仍然是如何最大化电路的输出功率。

负载的电压和电流的乘积决定了输送的功率。为了实现最大输出功率，应选择偏置点以最大化负载的电压和电流摆动。当晶体管被偏置在其有源区的中间时，实现最大摆动。为了找到合适的偏置点，我们为集电极支路写了一个KVL方程：

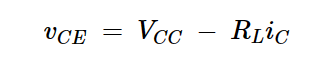
方程式1

其中：

iC是集电极电流总和

vCE表示集电极和发射极之间的总电压，包括直流和交流分量。

该方程式给出了电路的交流负载线，如图2所示。任何可能的iC值和相应的vCE值都落在交流负载线上。

共射极放大器的交流负载线。

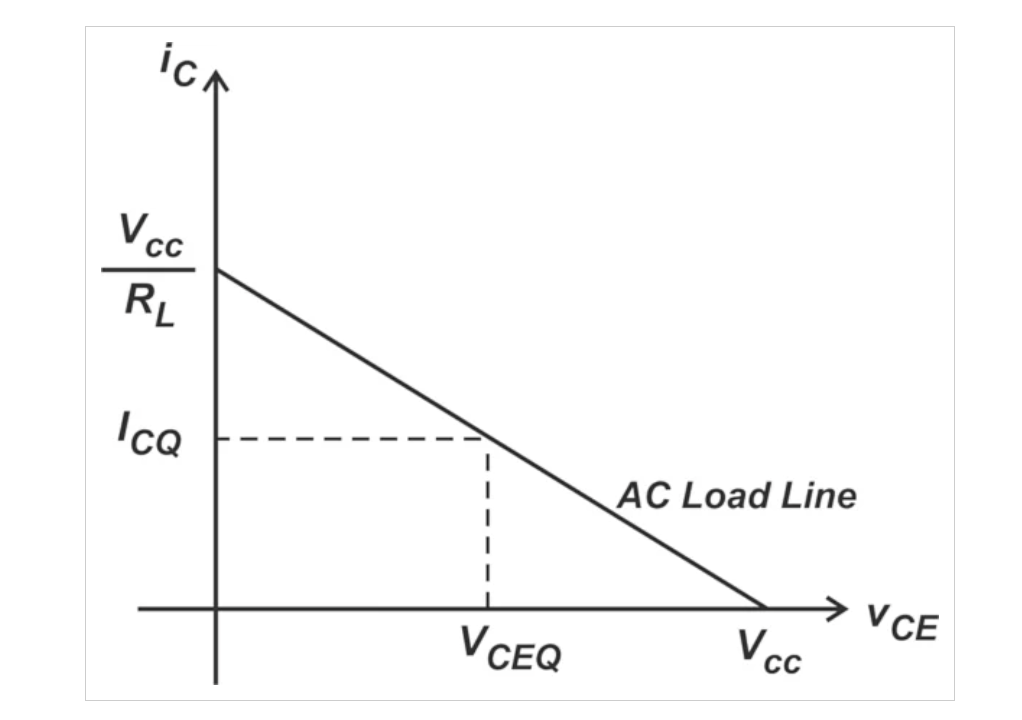
图2:共发射极电路的交流负载线。偏置点（ICQ和VCEQ）可以在两条虚线的交点处找到。

在我们的简单示例中，交流和直流负载线是相同的。这使得确定电压和电流限制变得容易——当晶体管处于截止状态（iC = 0）时，整个电源电压因此出现在集电极和发射极端子之间（vCE = VCC）。另一方面，对于饱和晶体管，集电极和发射极端子之间会出现非常小的电压降（通常为0.1 V）。忽略这个很小的电压降，我们找到了集电极电流的最大值：

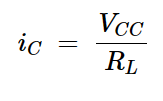
方程式2

交流负载线显示了电路中的电流和电压限制。通过将所采用特定类型的晶体管（BJT、FET等）的特性曲线叠加在交流负载线上，我们可以很容易地确定信号何时超过晶体管的线性范围。

为了获得最大摆动，我们选择交流负载线中间的偏置点（ICQ和VCEQ）。ICQ是静态集电极电流：

VCEQ是静态集电极-发射极电压：

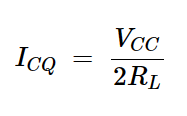
方程式3

VCEQ是静态集电极-发射极电压：

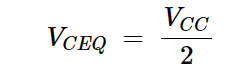
方程式4

因此，流经RL的峰值交流电流为：

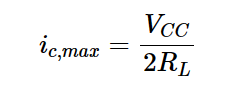
方程式5

换句话说，在最大输出功率的情况下，我们可以假设集电极电流由ICQ的偏置电流和振幅为ic，max的正弦电流分量组成：

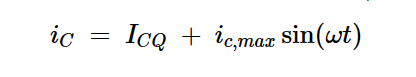
方程式6

其中⍵是交流信号的频率。

计算电源效率

传递给负载的功率有两个组成部分：来自偏置电流的直流功率和我们希望最大化的交流功率。由于我们知道集电极的峰值交流电流（ic，max），我们可以计算传递给负载的交流功率的平均值，如下式所示：

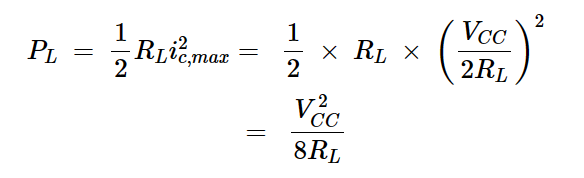
方程式7

请注意，这是负载的最大交流功率。当交流信号不存在时，向负载提供的交流功率为零。

我们可以使用以下方程计算电源电压提供的平均功率。方程6帮助我们创建右边的更复杂的版本，这将很快证明是有用的：

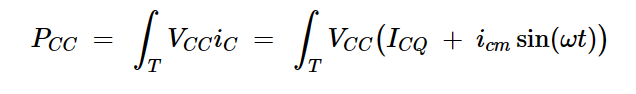
方程式8

其中T是信号的周期。

正弦项在一个周期内的平均值为零，因此方程8简化为：

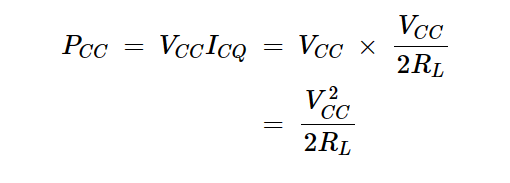
方程式9

ICQ的公式可以在方程式3中找到。

最后，使用方程式7和9，放大器的最大效率计算为：

向负载输送交流电

由电源提供的电力

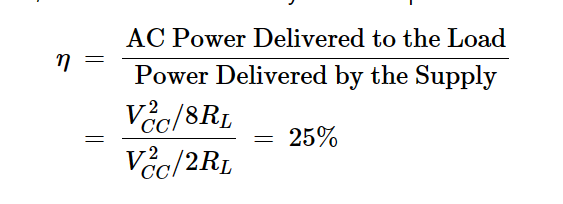
方程式10

这意味着电源必须提供4 W才能向负载提供1 W。额外的3 W的一部分在晶体管中损失；其余部分作为RL中的直流功率损失。在实践中，可实现的效率可能远低于25%。

现在我们知道如何计算最大效率，让我们找到最佳负载。

计算最佳负载

综上所述，方程式3和4表明，RL和晶体管的偏置点之间必须存在某种关系，以使晶体管达到最大输出功率。换句话说，对于给定的偏置条件，存在一个使输出功率最大化的最佳负载。

基于最大功率传输定理，我们可能会认为最佳RL取决于晶体管的输出阻抗。相反，它只取决于VCC和偏置点。这实际上是一个有趣（有时令人困惑）的点，但更详细的解释还有待另一天。现在，让我们考虑图3中的共发射极电路。

共发射极放大器，电源电压为12 V，静态电流为750 mA。

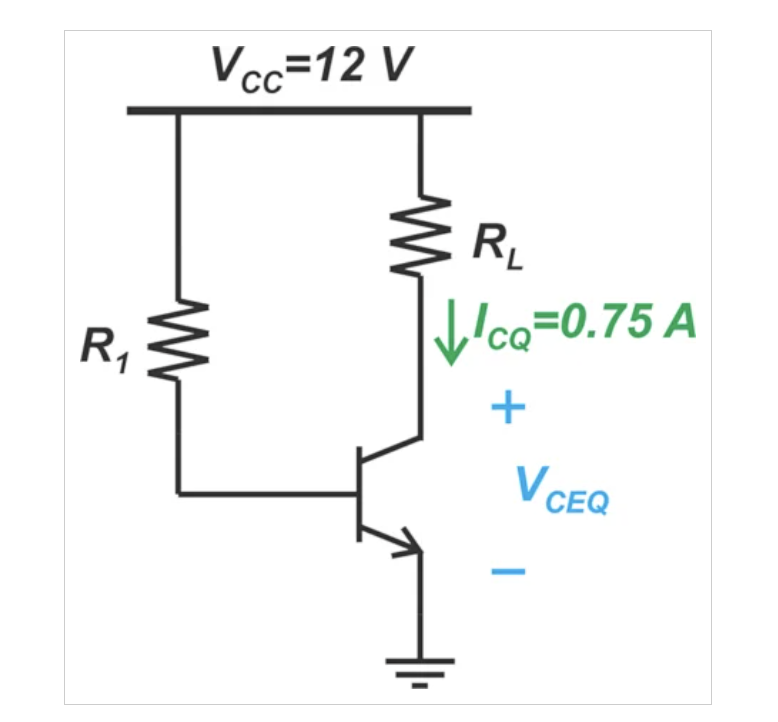
图3.电源电压为12V、静态电流为0.75A的共发射极放大器。

假设电源电压VCC=12V，静态电流ICQ=0.75A，RL的值是多少才能产生最大的输出功率？

我们通过重写方程3求解RL，得到最佳负载电阻的公式。

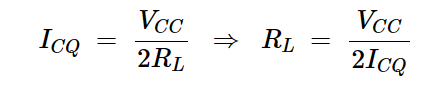
方程式11

对于上面给出的电源电压和静态电流值，计算结果为：

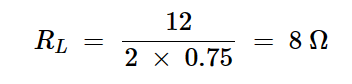
方程式12

图4显示了三个不同负载电阻值的负载线：RL = 4 Ω、8 Ω和13.33 Ω。该图帮助我们直观地了解给定静态电流的不同负载电阻如何产生不同的电压波动，从而产生不同的输出功率值。

三种不同负载电阻值的负载线，包括最佳值。

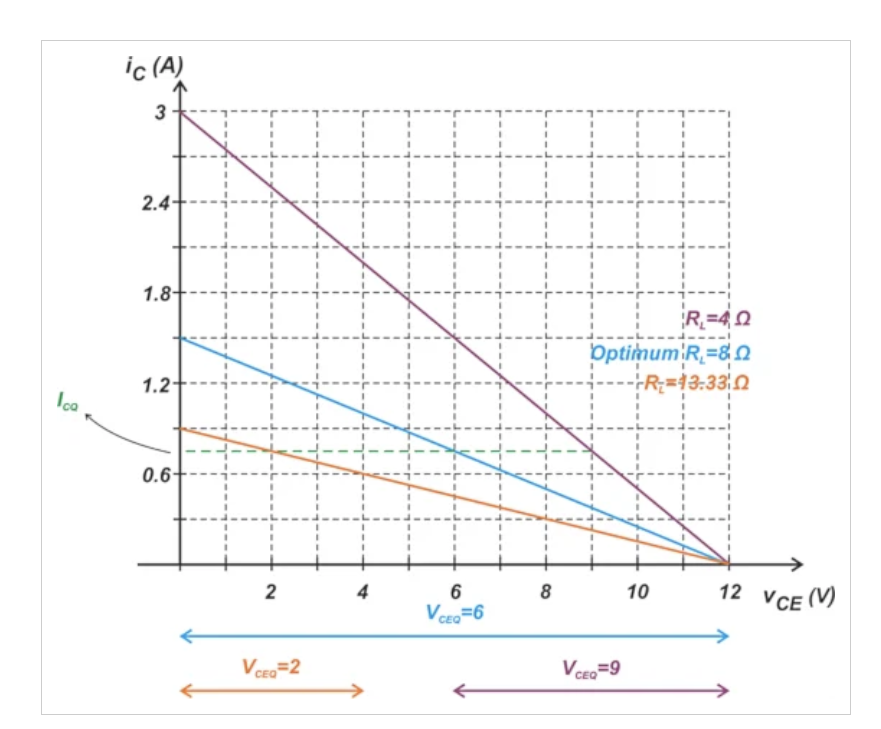
图4.三个不同负载电阻值的负载线：RL = 4 Ω（紫色），RL = 8 Ω（蓝色），RL = 13.33 Ω（橙色）。

结果：

当RL = 4Ω时，我们观察到在VCEQ = 9V时ICQ = 0.75A。在这种情况下，峰峰摆幅为6V（RL = 8Ω时摆幅的一半）。

最佳值RL=8Ω，导致VCEQ=6 V的直流收集器-发射器电压，该电压位于负载线的中间。

RL = 13.33 Ω导致VCEQ = 2 V，这再次产生了小于最佳值的峰间摆幅。

我们通过询问是否可以使用简单的共发射极级来有效地提供大量的输出功率，开始了本文的计算部分。答案似乎是“否”。但为什么呢？

共发射极级的缺点

通过简单的共发射极级，偏置电流始终流经负载。因此，仅仅为了偏置晶体管，负载中始终会浪费等于RLICQ2的直流功率。使用方程7，您可以验证此直流功率是我们能够提供给负载的最大交流功率的两倍。

这是电路效率低的原因之一。此外，我们计算的是最大可能的效率。如果交流信号低于最大摆幅，效率会进一步下降。

该电路的另一个缺点是，对于给定的电源电压，它提供的电压摆动相对较小。例如，考虑向50Ω天线输送1W射频功率的问题。如上所述，这需要提供20V的峰峰值电压摆动，以及通过天线的200mA峰值电流。

如图2中的交流负载线所示，最大峰峰值摆幅等于VCC。因此，我们需要大于20 V的电源电压才能为天线提供1 W的功率！许多便携式设备使用的电源电压要小得多。

电感负载A类功率放大器图5显示了一个更实用的A类放大器的基本原理图。该放大器通过使用电感负载和隔直电容来规避上述一些问题。

电感负载A类放大器的电路图。

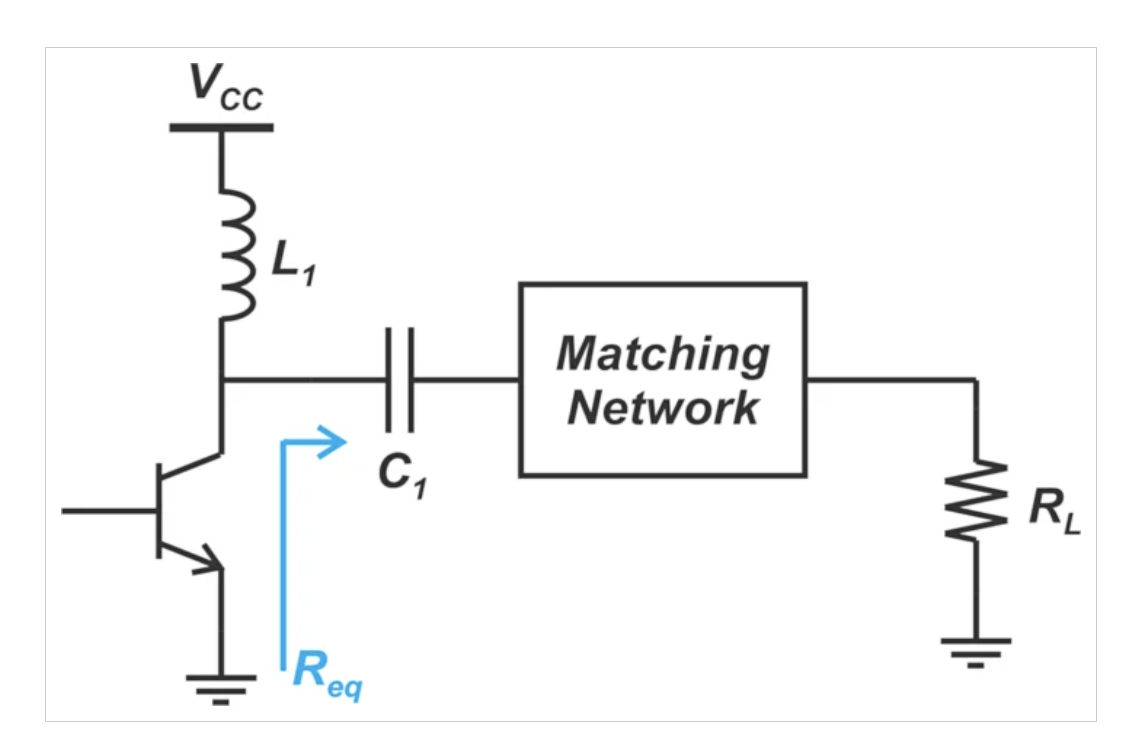
图5.电感负载A类放大器的基本示意图。

让我们来检查上述模型的标记部分。

RL是电阻器。它代表我们希望为其供电的实际负载。

L1是电感器。它足够大，可以在感兴趣的频率下充当交流开路电路——我们称这种电感器为“RF扼流圈”。

VCC是电源电压。正如我们在下一篇文章中看到的，电感负载级可以有对称的电压摆动，其值是VCC的两倍。

Req是使输出功率最大化的最佳负载。

C1是电容器。它阻断直流电流，但在感兴趣的频率下充当交流短路。

匹配网络用于将RL转换为Req。由于匹配网络几乎总是使用电抗元件（电感器和电容器）来实现，因此传输到匹配网络输入端的功率会在RL中耗散。为了防止RL中的任何直流耗散，集电极通过C1连接到匹配网络。如上所述，C1用于阻断直流电流。

在本系列的下一篇文章中，我们将继续更深入地讨论电感负载A类放大器。