0   引言

全自动是针对国际先进封装工艺——倒装工艺所研制的专用封装设备，此设备所生产出的芯片处理数据速度快、体积小、功能多、耗电量小、成本低，是集成电路芯片向小型化、智能化发展的必然趋势。主要应用在无线局域网络天线、系统封装、多芯片模块、图像传感器、微处理器、医用传感器以及无线射频识别等等领域^[1]。此技术替换常规打线接合，使封装后的芯片体积革命性减小，同时，产品性能大幅度提高。

全自动是封装大规模集成电路（IC）的专用封装设备，是一种集机械、电气控制、软件、图像识别、光学、材料以及热学等多学科交叉的高科技产品，目前国外只有少数几家技术领先的公司可以研发出此类设备，如瑞士的Besi 集团与新加坡的ASM 公司等。

本文针对贴装位置修正补偿，来达到焊凸（Solder Bump）位置精度的提高。采用先测量的垂直度，通过R 旋转轴和上照视觉系统检测不同角度下，视觉系统给出的数据，根据数据计算，在贴装过程中补偿旋转角度引起的XY 方向偏差值进行修正后，提高了全自动倒装贴装机的贴装精度和每小时的产出量（UPH）。

全自动倒装贴装机的广泛应用将大大降低芯片生产成本，促进我国集成电路封装产业的健康发展，并带动产业链上下游企业共同发展，全方位地提升我国集成电路产业的整体竞争优势。

1   贴装精度的重要性

随着高密度化、微型化、轻薄化、高集成化成为新一代芯片的发展趋势，具备互连长度低、减小干扰、降低容抗、尺寸超小、成品率高、成本低等技术优势的倒装芯片技术成为了新的发展热潮。

随着时间推移，高性能芯片的焊凸（Solder Bump）数量不断提高，基板变得越来越薄，要获得满意的装配良率，贴装精度要求越来越高。对于焊凸间距小到0.1 mm 的器件，不考虑其他因素的影响，只讨论机器的贴装精度。建立一个简单的假设模型^[2]：

1）假设倒装芯片的焊凸为球形，基板上对应的焊盘为圆形，且具有相同的直径；

2）在回流焊接过程中，器件具有自对中性，焊凸与润湿面50% 的接触在焊接过程中可以被“拉正”。

那么，基于以上的假设，直径25 μm 的焊凸如果其对应的圆形焊盘的直径为50 μm 时，左右位置偏差（X 轴）或前后位置偏差（Y 轴）在焊盘尺寸的50%，焊凸都始终在焊盘上，对于焊凸直径为25 μm 的倒装芯片，工艺能力Cpk 要达到1.33 的话，要求设备的最小精度必须达到12 μm @3sigma。所以全自动倒装贴装机的贴装精度成为了设备的主要性能指标。

2   系统结构及实现过程

全自动倒装贴装机采用动臂式结构，X 轴运行采用完全同步控制回路的双伺服电动机驱动系统，加快运动速度，防止悬臂梁的效应，减少机械稳定时间；Y 轴Z轴R 轴采用高定位精度和高重复精度的直线电动机，采用模糊控制技术，运动过程中分3 段控制，即“慢—快—慢”，呈“S”型变化，从而使运动变得既“柔和”，又快速。视觉系统分为上照视觉系统和下照视觉系统，下照视觉系统随电机轴运动，主要用于获取目标贴片位置关联的特征点，上照视觉系统主要对、芯片和焊凸等特征点进行识别，从而建立坐标关系^[3]。

当贴装头拾取芯片完成后，移动到上照视觉系统上检测芯片拾取姿态，根据上照视觉系统数据给出的特征点XY 及角度偏差。如图1 所示。

由于贴装头拾取芯片位置不能完全固定在贴装头，贴装杆垂直度不能完全保证完全垂直等原因，造成上照视觉系统给出数据在使用中有较大偏差。

3   基于误差的补偿方法

基于以上出现问题，需要解决两个问题。

1）通过坐标变换后，得到新的XY 及角度的补偿数据。

2）精准找到贴装头的旋转中心。

问题1）是个算法问题，坐标系内一个点（x0，y0）绕一点（a，b）旋转一定角度θ 之后的坐标（x，y）可由算法公式

得出

问题2）的难点在于如何准确的找到贴装头的旋转中心。

①根据单个圆圆心坐标的拟合思路，设定圆心坐标位（x₀，y₀），半径为R，测量出的n 个坐标点，坐标位（x_i，y_i），i = 1，2，3…n 推算公式如下。

最小二乘法拟合圆曲线的基础方程^[4]

展开式（4）可得

另a=2x₀，b=2y₀，c=x₀²+y₀²-R²，由式（5）变换之后有

x²+y²-ax-by+c=0   （6）

将式（6）推广到n 个点后，写成矩阵形式可得

由式（7）两边同时乘以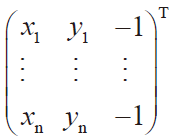进行矩阵变换^[5]可得

解出a，b，c，带入到x₀=a/2，y₀=b/2，，可求出旋转中心（x0，y0）和半径R。

②最小二乘法拟合圆的方法对误差符合正态分布的数据点效果比较好。但是在视觉系统应用中经常会碰到一些干扰点。这时要是用最小二乘法拟合，拟合出的圆可能会有偏差。因此，根据任意不在同一直线上的3 点确定1 个圆，所有确定的圆心到其所有点的距离最短，来确定圆心坐标及半径。

我们设一个圆的圆心坐标为（x0，y0），半径为r。那么这个圆的方程可以写为：

在这个圆上随便取3 个点，设这3 个点的坐标分别是（x₁，y₁），（x₂，y₂），（x₃，y₃），那么有：

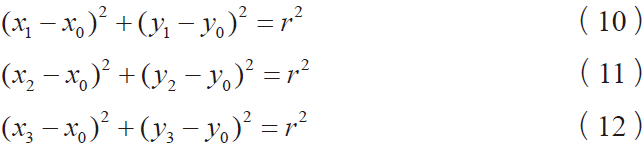
式（10）（11）相减，（10）（33）相减之后经过化简可以得到：

有唯一解的条件是3 点不能共线。设：a = x₁-x₂；

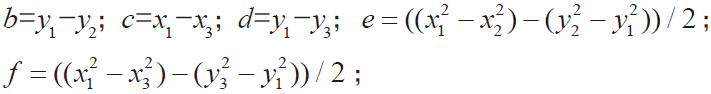
那么：

根据多组圆心求圆心（x_0i，y_0i），i = 1，2...n 到所有点（x_i，y_i）的距离最小值。

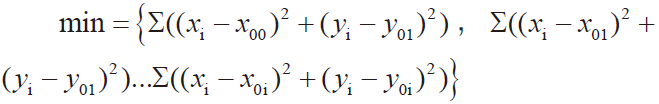
通过以上分析，现采用贴装头旋转36° 每1° 使用上照系统进行数据采集，共采集36 组数据单位为毫米，数据结果如表1。

通过编程软件程序结果运算后，利用最小二乘法计算圆心坐标x₀=0.1431167，y₀=0.1049344， 半径R=0.2079683。利用不同3 点进行圆心计算后，再计算每个圆心到其他点距离和的最小值，确定最终圆心坐标x₀=0.1457283，y₀=0.1043651，半径R=0.2067638。

进行重复数据采集后，上照视觉系统给出数据误差在2 μm 毫米范围内，通过编程软件运行结果后，对比圆心坐标值计算最短距离最小值的方法比最小二乘法的方法影响更小，并且圆心坐标和半径数据影响不大，可以忽略不计。

4   试验结果与分析

贴装头在取片过程中所使用角度有限，一般都在±5°之内，所以在±6°进行多组测试实验，首先贴装头X 轴Y 轴在上照视觉系统固定位置，使R 轴在不同角度下，进行视觉系统采集数据，根据视觉系统给出数据，通过编程软件对两个旋转中心坐标进行计算，在使旋转R 轴为零，对比R 轴旋转为零时的数据。并进行多组相同数据验证。

从表2 部分数据对比表中可以看出根据最小二乘法计算和最短距离计算出的XY 偏差值很接近，最大差值相差5 μm，但是全自动倒装贴片机对精度要求非常高，所有还需要和实际轴运动后的偏差值进行比较。通过和角度为零后数据比较，最短距离的方法和实际情况更加接近，拟合出来的原点坐标值更加准确。

通过此方法可以更加准确地找到贴装头的旋转中心，使贴片精度比最小二乘法拟合圆的方法至少有了1 μm 的提升，并且几乎不受干扰点影响。

通过此方法优化后的设备减少了拍照次数和在上照视觉系统上停留的时间提高了整体的UPH 和精度。

5   结束语

本文分析了全自动倒装贴装机对贴装精度的重要性，并对芯片在上照视觉系统上可能出现的精度误差进行分析和优化。最后将两种算法应用到设备中，对比了不同算法对旋转中心和芯片中心不同，旋转角度引起的XY 方向偏差，继而对贴装精度的影响。

通过实际验证，不同3 点进行圆心计算后，在计算每个圆心到其他点距离和最小值的方法更能精准地找到贴装头旋转中心，并且在一定条件下，减少测点误差对旋转中心的影响。算法具有可行性和科学性，提高了贴装精度和效率，缩短了贴装时间，实现了高精度贴装机贴装位置补偿功能。

参考文献：

[1] 周德俭.国产贴片机研发现状与分析[J].电子机械工程, 2016,32(1):1-4.

[2] 李忆.Fc装配技术.电子电路与贴装[J].2007(6):33-38.

[3] 程海林.贴片设备的关键技术及现状.电子工业专用设备[J].2020,49(2):7-11.

[4] 石振东.误差理论与曲线拟合[M].哈尔滨:哈尔滨工程大学出版社,2010:201-203.

[5] 同济大学数学系.线性代数[M].北京:北京高等教育出版社,2009:57-65.

（本文来源于《电子产品世界》杂志2022年12月期）