一、概述

当处理数据时，常常会遇到缺失数据的情况。缺失数据可能由于各种原因引起，例如传感器故障、人为错误、数据采集问题等。对于数据分析和建模任务来说，缺失数据可能会导致结果不准确或无法进行有效分析。因此，重建缺失数据是数据预处理的重要步骤之一。

二、缺失数据的重建

缺失数据的重建是通过利用已有的数据信息来推断和填补缺失数据点。下面将介绍几种常见的缺失数据重建方法：

删除缺失数据：当缺失数据量较大或缺失数据对分析结果影响较大时，可以选择删除缺失数据所在的样本或特征。这种方法的优点是简单直接，但可能导致数据集的减少和信息损失。

（1）均值、中位数或众数填补：这是最简单的缺失数据重建方法之一。对于数值型数据，可以使用均值、中位数或其他统计量来填补缺失值；对于分类型数据，可以使用众数来填补缺失值。这种方法的优点是简单快速，但可能忽略了样本间的差异性。

（2）插值法：插值法是一种常用的数据重建方法，它基于已有数据点的关系来估计缺失数据点的值。常见的插值方法包括线性插值、多项式插值、样条插值等。插值方法可以在一定程度上保留数据的趋势和变化特征。

（3）回归方法：回归方法是利用已有数据的特征和标签信息来建立回归模型，然后利用模型预测缺失数据点的值。常见的回归方法包括线性回归、岭回归、随机森林回归等。回归方法适用于有较多相关特征的数据集。

（4）使用机器学习方法：机器学习方法可以应用于缺失数据的重建。可以使用监督学习算法如决策树、支持向量机、神经网络等来预测缺失数据点的值；也可以使用无监督学习算法如聚类、主成分分析等来估计缺失数据点。

需要注意的是，选择合适的缺失数据重建方法需要根据具体问题和数据特点进行评估。不同的方法可能适用于不同的数据集和任务。在进行缺失数据重建时，还要注意评估重建后数据的准确性和合理性，避免引入额外的偏差或误差。

三、插值法Python示例

# coding utf-8

from scipy.io import loadmat

import numpy as np

from numpy import ndarray

from scipy.interpolate import interp1d

import matplotlib.pyplot as plt

def get_data(data_path, isplot=True):

    data = loadmat(data_path)

    t_true = data['tTrueSignal'].squeeze()

    x_true = data['xTrueSignal'].squeeze()

    t_resampled = data['tResampled'].squeeze()

    # 对数据进行抽取(间隔100抽样)

    t_sampled = t_true[::100]

    x_sampled = x_true[::100]

    if isplot:

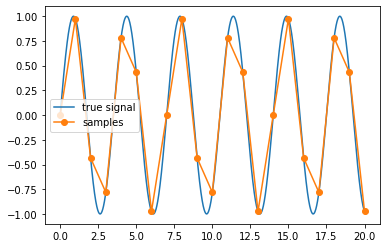
        # 绘制数据对比图1

        plt.figure(1)

        plt.plot(t_true, x_true, '-', label='true signal')

        plt.plot(t_sampled, x_sampled, 'o-', label='samples')

        plt.legend()

        plt.show()

    return t_true, x_true, t_sampled, x_sampled, t_resampled

def data_interp(t, x, t_resampled, method_index):

    if method_index == 1:

        # 返回一个拟合的函数(线性插值)

        fun = interp1d(t, x, kind='linear')

    elif method_index == 2:

        # 返回一个拟合的函数(三次样条插值)

        fun = interp1d(t, x, kind='cubic')

    else:

        raise Exception('未知的方法索引,请检查!')

    # 计算值

    x_inter = fun(t_resampled)

    return x_inter

def result_visiualize(x_inter_1, x_inter_2):

    # 加载数据

    t_true, x_true, t_sampled, x_sampled, t_resampled = get_data('./data.mat', isplot=False)

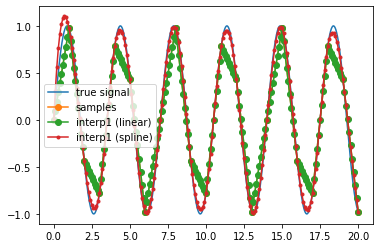
    plt.figure(2)

    plt.plot(t_true, x_true, '-', label='true signal')

    plt.plot(t_sampled, x_sampled, 'o-', label='samples')

    plt.plot(t_resampled, x_inter_1, 'o-', label='interp1 (linear)')

    plt.plot(t_resampled, x_inter_2, '.-', label='interp1 (spline)')

    plt.legend()

    plt.show()

if __name__ == '__main__':

    # 加载数据

    t_true, x_true, t_sampled, x_sampled, t_resampled = get_data('./data.mat')

    # 进行插值

    x_inter_1 = data_interp(t_sampled, x_sampled, t_resampled, method_index=1)

    x_inter_2 = data_interp(t_sampled, x_sampled, t_resampled, method_index=2)

    # 绘制图片

    result_visiualize(x_inter_1, x_inter_2)

四、总结

总结起来，在处理缺失数据时，我们可以选择不同的重建方法，如删除缺失数据、均值填补、插值法、回归方法和机器学习方法。每种方法都有其优点和适用场景，需要根据具体情况进行选择。

删除缺失数据的方法简单直接，适用于缺失数据量较大或对结果影响较大的情况。然而，这种方法可能会导致数据集的减少，从而可能影响后续分析的准确性和可靠性。

均值填补是一种常用的方法，适用于数值型数据。可以计算特征的均值或中位数，并用这些值来填补缺失数据点。这种方法的优点是简单快速，但可能忽略了样本间的差异性。

插值法是一种基于已有数据点关系的方法，用于估计缺失数据点的值。常见的插值方法包括线性插值、多项式插值和样条插值。插值方法可以在一定程度上保留数据的趋势和变化特征。

回归方法是利用已有数据的特征和标签信息来建立回归模型，然后利用模型预测缺失数据点的值。这种方法适用于具有相关特征的数据集。常见的回归方法包括线性回归、岭回归和随机森林回归。

机器学习方法可以应用于缺失数据的重建。可以使用监督学习算法如决策树、支持向量机和神经网络来预测缺失数据点的值，也可以使用无监督学习算法如聚类和主成分分析来估计缺失数据点。

在选择重建方法时，需要考虑数据的特点、缺失数据的类型和任务的要求。还要注意评估重建后数据的准确性和合理性，避免引入额外的偏差或误差。

最后，对于缺失数据的重建，没有一种通用的方法适用于所有情况。根据具体的问题和数据特点，我们需要灵活选择适合的方法，并结合领域知识和经验进行评估和调整，以获得可靠和准确的重建结果。