一、有限状态机定义
有限状态机(Finite-State Machine,FSM),又成为有限状态自动机,简称状态机,是表示有限个状态以及在这些状态之间的转移和动作等行为的数学模型。本文所讲的是基于硬件描述语言Verilog HDL的有限状态机的编写技巧及规范。众所周知FPGA以其并行性和可重构性为世人所知,而在当今的电子世界,基本所有的器件都是串行的,所以作为控制单元或者是可编程单元的FPGA需要进行并行转串行与外界进行通信、控制等,而有限状态机以其简单实用、结构清晰而恰如其分的充当着这个角色。
有限状态机是由寄存器组和组合逻辑构成的硬件时序电路,其状态(即由寄存器组的1和0的组合状态所构成的有限个状态)只可能在同一时钟跳变沿的情况下才能从一个状态转向另一个状态,究竟转向哪一状态还是留在原状态不但取决于各个输入值,还取决于当前所在状态。
二、设计思想:
状态机的本质是对具有逻辑顺序或时序规律事件的一种描述方法。这个论断的最重要的两个词就是“逻辑顺序”和“时序逻辑”,这两点就是状态机所要描述的核心和强项,换言之,所有具有逻辑顺序和时序规律的事情都适合用状态机描述。
状态机的两种应用思路。第一种思路,从状态变量入手。如果一个电路具有时序逻辑或者逻辑顺序,我们就可以自然而然地规划出状态,从这些状态入手,分析每个状态的输入,状态转移和输出,从而完成电路功能;第二种思路,需要首先明确电路的输出关系,这些输出相当于状态的输出,回溯规划每个状态,和状态转移条件与状态输入。两种思路殊途同归,都要通过使用状态机的目的来达到控制某部分电路的目的,完成某种具有逻辑顺序或时序规律的电路设计。
在设计状态机之前首先应该画出问题的状态转移图,状态转移图的例子如下所示:
三、状态机分类:
(1):mealy型和moore型
状态机有两大类:Mealy型和Moore型。Moore型状态机的输出只与当前状态有关,而Mealy型状态机的输出不仅取决于当前状态,还受到输入的直接控制,并且可能与状态无关,其状态机结构请看下图:

Mealy型状态机结构图
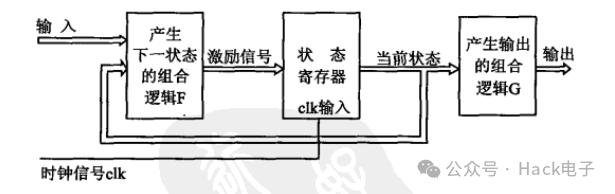
Moore型状态机结构图
(2):按照状态编码来分类:
1、Gray(格雷码)码状态机
2、one-ho码(独热码)状态机
3、二进制码状态机
详解:
有限状态机编码时采用格雷码和采用独热码的选择
格雷码:相邻之间只变1bit,编码密度高。
独热码:任何状态只有1bit为1,其余皆为0,编码密度低。
比如说,表示4个状态,那么状态机寄存器采用格雷码编码只需要2bit:00(S0),01(S1),11(S2),10(S3);
采用独热码需要4bit:0001(S0),0010(S1),0100(S2),1000(S3)。所以很明显采用格雷码可以省2bit寄存器。
难理解的是,为什么独热码更节省组合逻辑:
其实很简单,
例一:
假如我们要在代码中判断状态机是否处于某状态S1,
对于格雷码的状态机来说,代码是这样的:assign S1 = (STATUS==2'b01);
对于独热码来说,代码是这样的就行:assign S1=STATUS[1];
所以独热码的译码非常简单。
例二:
考虑最简单的跳变,当A为1时,状态机会从S0跳到S1:。
采用格雷码写:
STATUS[1:0] <= (STATUS==2'h00) & A ? 2'h01 : 2'h00; 采用独热码写: STATUS[1] <= STATUS[0] & A; 有人怀疑这里的逻辑,认为只check独热码的一个bit有问题。当然是没问题的,0110,0011等编码属于不care的编码,在卡诺图化简中,不care的编码可以与其余的有效编码合并化简。实际上综合器也会这么做,所以独热码非常容易化简。假如说S0跳到S1条件为A;S1跳到S2条件为B;S2跳到S3条件为C;S3跳到S0条件为D;那么整个状态机 化简之后代码就是: STATUS[0] <= STATUS[3] & D; STATUS[1] <= STATUS[0] & A; STATUS[2] <= STATUS[1] & B; STATUS[3] <= STATUS[2] & C;
总结一下:
独热码适合写条件复杂但是状态少的状态机;
格雷码适合写条件不复杂但是状态多的状态机。
独热码 使用的触发器较多,但可减少实现状态机的组合逻辑数目,减少复杂性,提高系统的速度,即工作时钟频率可以做到最高。格雷码是使用最小数目的触发器来编码状态机,但形成的组合逻辑比较复杂。
使用独热码编码时,会出现很多未使用的状态,而使用二进制编码和格雷码编码时,如果状态机的状态数不是2的指 数 次方时,也会出现未使用状态。
格雷码每个相邻的状态切换只有一个bit的信号跳变,适用于异步握手的情况,比如异步FIFO的指针计数。
(3):在Verilog中描述有限状态机,可以有三种形式,可分为一段式、二段式和三段式。这三种描述主要根据其输入、输出和状态来分类。
一段式状态机:一段式状态机只选择一个状态标志位,这个状态标志位会在输入的决定下选择跳转到下一个状态还是维持原有状态,在每一个状态下检测状态标志位及输入来决定其状态的跳转及输出。其输出和状态的切换在一个always循环块中执行。
eg:
always()begin S0:begin state = (in)?S0:s1;out = ;end S1:begin state = (in)?S1:s2;out = ;end S2:.....................................end
二段式状态机:二段式状态机将状态分为当前状态和此状态,其系统会自动将次状态更新到当前状态,其输入更新在次状态上,其决定系统的状态切换和输出。其输出和状态的切换在两个个always循环块中执行,第一个always块决定系统状态标志的自动跳转,第二个always块决定系统根据不同状态下的输入进行状态的跳转及输出。
eg:always() begin state=next_state end always() begin S0:begin next_state = (in)?S0:s1;out = ;end S1:begin next_state = (in)?S1:s2;out = ;end S2:..................................... end
三段式状态机:二段式状态机将状态分为当前状态和此状态,其系统会自动将次状态更新到当前状态,系统的输入更新在次状态上,其决定系统的状态切换,系统会根据其当前状态决定输出的值。其输出和状态更新和状态切换在三个always块中,第一个always块决定系统状态标志的自动跳转,第二个always块决定系统根据不同状态下的输入进行状态的切换,第三个always块根据系统的当前状态决定输出的值。
eg:always() begin state=next_state end always() begin S0:next_state = (in)?S0:s1; S1:next_state = (in)?S1:s2; S2:..................................... end always() begin S0:out = ; S1:out = ; S2:..................................... end
(4),三段式状态机子详细解释:
摩尔状态机的架构

状态转换图
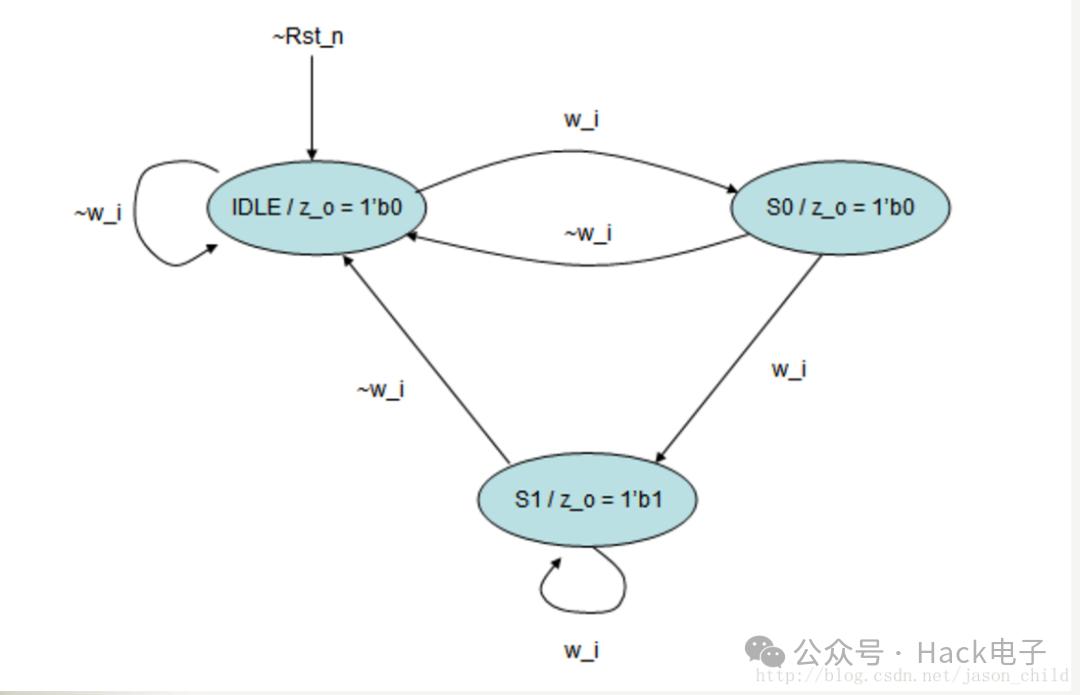
module finite_fsm( z_o, clk, Rst_n, w_i ); //输出端口 output z_o; //输入端口 input clk; input Rst_n; input w_i; //输出端口类型声明 reg z_o; //参数声明 parameter IDLE = 2'b00; parameter S0 = 2'b01; parameter S1 = 2'b10; //内部信号声明 reg[1:0] current_state; reg[1:0] next_state; //状态寄存器 always @ (posedge clk or negedge Rst_n) begin if(!Rst_n) current_state <= IDLE; else current_state <= next_state; end //次态的组合逻辑 always @ (w_i or current_state) begin case(current_state) IDLE:begin if(w_i) next_state = S0; else next_state = IDLE; end S0: begin if(w_i) next_state = S1; else next_state = IDLE; end S1: begin if(w_i) next_state = S1; else next_state = IDLE; end default : next_state = 2'bxx; endcase end //输出逻辑 always @ (*) beign case(current) IDLE: z_o = 1'b0; S0: z_o = 1'b0; S1: z_o = 1'b1; default: z_0 = 1'b0; endcase end endmodule
关于三段式状态机的一点总结
1确定输入输出信号,及其类型(是wire还是reg);
2声明内部信号,一般需要定义current_state和next_state;
3用3个always语句描述状态机;第一个用来次态和现态的转换,第二个always用于现态在输入情况下转换为次态的组合逻辑;第三个语句用于现态到输出的组合逻辑输出。
