0 引言

作为一项重要可用于恢复样品高分辨率和相位的技术，近几年来傅里叶叠层成像(FP) 取得显著进步^[1,2]。样品高分辨率成像在大视场下完成的主要原因是具有相对较为简单的运行设施及FP 技术所需算法，实现的功能还包括三维重聚焦^[3,4]。在处理稀疏矩阵时应用协同过滤算法，该算法基于内存分析完成建立，所以系统准确预测及高效运行均不能得到充分有效保障，此问题需将新算法引入完成处理，将原传统算法进行改进。在推荐算法中早已应用SVD 技术，表现出较强的降维性能，结果显示可显著改善数据稀疏性^[5]。最初在搜索潜在语义领域应用SVD 技术，该算法被应用于推荐算法中，确定维数完成预测前，需按照含有奇异值对角矩阵、用户特征向量矩阵、低维项目特征向量矩阵分解高维用户- 项目评分矩阵，维数确定需结合奇异值大小及数量^[6]。

本文获取ELM 算法采用K-SVD 处理实现，并成功应用于多特征融合物体成像识别领域。

1 ELM改进

1.1 SVD梯度下降法

针对以SVD技术为基础的推荐算法，应用梯度下降法获取的优化效果较佳，优化原理为：将点集(X, Y)预先设置，特征变量及预测值分别对应X 和Y 变量，通过迭代学习对某X 特征采用机器学习模式查询获取估计函数，然后再获取估计值Y，通过该函数预测新数据^[7]。设定点集X 内第n 个特征分量为x_n，构建变量X = (x₁,x₂, ... x_n)，拟合函数h(x) 表达式为：

h(x)=a₀+a₁x₁+a₂x₂+...a_nx_n

式中，a 参数需通过迭代运算求解。同时判断真实值与预测值间的差异时需利用误差函数，利用该算法迭代求解，用以下形式表示该误差函数：

J(a)=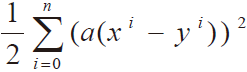   （1）

然后最小化J(a)，求解最小J(a)主要依据各a值完成。用一个曲面或一条曲线代替J(a)，同时参考数学分析理论基础，通过计算曲面或最低点替代最小值求解问题^[8]。然后以最快速度并结合梯度最大方向完成最值搜索，求导J(a)后再按上述步骤进行求解。按照以下形式调整a表达式：

a _i - J(a) = a _i - α(h(x) - y)x_i   （2）

学习效率高低用α表示，操纵迭代步长，最佳效果在未合理控制此参数的情况下将难以达到。

按照以下步骤应用梯度下降法完成计算：

第1步：确定初始值h 及误差阈值ε，同时要求ε ＞ 0。

第2步：最小化误差函数J (a)，然后再求解下降方向，计算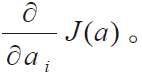

第3步：判断J(a)是否比ε小，将计算结果输出；否则则按上述步骤进行重新计算。

1.2 训练ELM算法

训练DELM-AE 算法的流程图如图1所示。在测试样本稀疏编码过程中，所利用字典选用全部的测试样本，测试样本标签值的判定则需依据重构误差最小准则。训练算法数据传输模式在隐含层及输入均选用全连接模式，学习参数用β 表示。同时选用单隐层ELM算法解析算法各层及前一层，有利于训练成本的大幅降低，单隐层ELM“输入层”用“输出层”代替。参考此方法可完成极限学习机网络模型的构建，实现自编码功能，训练参考以上步骤进行。

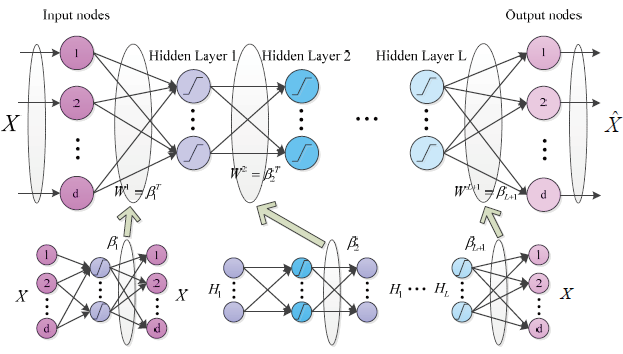
图1 ELM改进流程图

2 物体识别的应用

2.1 物体识别

在Coil-20 数据集中验证ELM 算法。旋转10°后再对每个物体进行照片采集，共计获得36×20 张图片。采用随机方式，在识别物体的过程中进行训练选取图片为18×20 个，专门用于测试的样本数据为剩余图片。

基于3 层ELM 算法完成隐含层节点在K-SVD 算法中的设定，然后完成20 个节点的选取，各个节点识别率在ELM 算法隐含层中的测试结果如表1所示。

表1 ELM算法的识别率

为全方位评价字典学习结果，K-SVD 学习字典情况依据ELM 算法获取，具体结果见图2。通过ELM 算法，同时结合图2 详细数据，字典精确度和优势在处理后的提升效果均十分显著。

图2 经过ELM预处理前后的字典

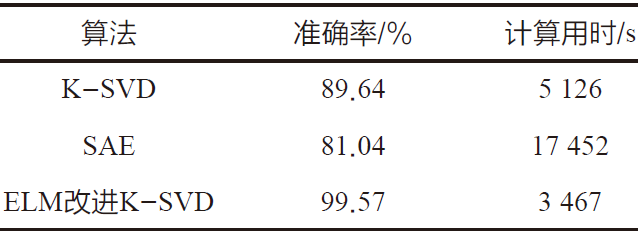
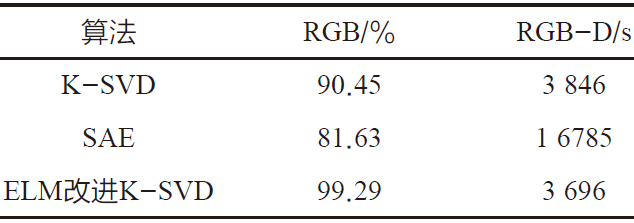
对比分析表2数据，发现应用不同算法获取的计算准确率不同，包括、SAE 算法及ELM 算法。数据结果显示，从收敛速度来看，K-SVD 算法相对较快，同时相比SAE 算法，该算法的收敛时间更短。因此，不论是从计算效率还是计算准确率来看，相比于ELM算法，改进的K-SVD算法表现出较佳的性能优势。

表2 Coil-20的实验结果

2.2 多特征融合的物体识别

本实验采集数据环节抓取目标数据集时应用的机械臂由康奈尔大学机器研究实验室开发而成。由8 005 张图像及260 个对象构成数据集，图像拍摄和存储利用Kinect，利用机械臂抓取目标，按特定方向和适当的背景点云摆放各对象和设置各图像。同时按照24×24 的尺寸标准调整设置图像像素大小，任何彩色与深度的图片都涵盖在内，2 304 维的目标由各机械臂抓取，576维深度特征及1 728 维RGB 特征均包含在内。

经实验测试得到，共有3 个节点数均为100 的隐含层包含在ELM 网络模型中，识别效果良好，计算准确率结合实验测试结果最终为90.1%；参数条件设置一致，仅有RGB 特征存在的情况下，识别率仅为83.1%。参考上述分析得出，系统识别精度在应用深度特征后得到显著提升。本实验测试的具体结果可参考表3 与表4数据。

表3 三个隐含层ELM改进K-SVD算法识别率统计

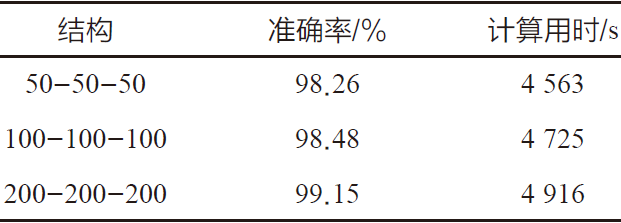
对比分析表3数据得出，实验过程中采用K-SVD算法但未应用深度信息的情况下， 识别准确率为76.3%，该项参数数据在使用深度特征信息后有显著提升，可达到81.4%的识别准确率；当深度信息匮乏的情况，ELM识别率为81.5%；新增深度信息后则增长至82.9%；除此之外，在对原始图像融合特征进行处理的过程中，将ELM 网络模型引入到前端，即使应用传统K-SVD算法也能获取89.83% 准确率较高的识别率，但是识别准确率在深度信息未涵盖的情况下仅为83.9%。K-SVD 算法性能可通过ELM 得到显著提升，当然算法识别准确率在多特征加入后也相应得到快速增长。

表4 多特征融合结果对比

将较低分辨率的样本从图像中筛选出来，然后再将其分辨率进行恢复，有利于减少傅里叶叠层成像数量。

3 结束语

本文开展基于ELM 改进K-SVD 算法的多特征融合物体成像识别分析，得到如下有益结果：

1）不论是从计算效率还是计算准确率来看，改进的K-SVD 算法表现出较佳优势。

2）K-SVD 算法性能可通过ELM 显著提升，算法识别准确率在多特征加入后也相应快速增长。

参考文献：

[1] 何承刚,朱友强,王斌.基于粒子群优化的宏观傅里叶叠层成像位置失配校准[J].光学精密工程,2022,30(23):2975-2986.

[2] 宋东翰,王斌,朱友强,等.基于多尺度特征融合网络的傅里叶叠层成像[J].液晶与显示,2022,37(11):1476-1487.

[3] 浦东,何小亮,戈亚萍,等.基于宏观傅里叶叠层成像技术的光学传递函数测量[J].光学学报,2022,42(14):117-124.

[4] CHAMARA L L, ZHOU H, HUANG G B. Representational learning with ELMs for big data[J]. Intelligent Systems,IEEE,2013, 28(6):31-34.

[5] WIDROW B, GREENBLATT A, KIM Y, et al. The no-prop algorithm: a new learning algorithm for multilayer neural networks[J]. Neural Networks the Official Journal of the International Neural Network Society,2013,37(1):182-188.

[6] 毛海锋,赵巨峰,崔光茫,等.基于傅里叶叠层显微成像的LED阵列位置校正方法[J].光学学报,2021,41(4):103-113.

[7] 沙浩,刘阳哲,张永兵.基于深度学习的傅里叶叠层成像技术[J].激光与光电子学进展,2021,58(18):374-383.

[8] 胡跃辉,房国庆,方勇,等.基于凸优化的傅里叶叠层成像技术研究[J].应用光学, 2021, 42(4): 651-655.

（本文来源于《电子产品世界》杂志2023年8月期）