在DCDC电源设计过程中，反馈电阻的选取需要考虑什么因素？取值的大小对电源会造成什么影响？本文就板卡DCDC上遇到的问题展开对此的探讨
文章目录
1 问题描述
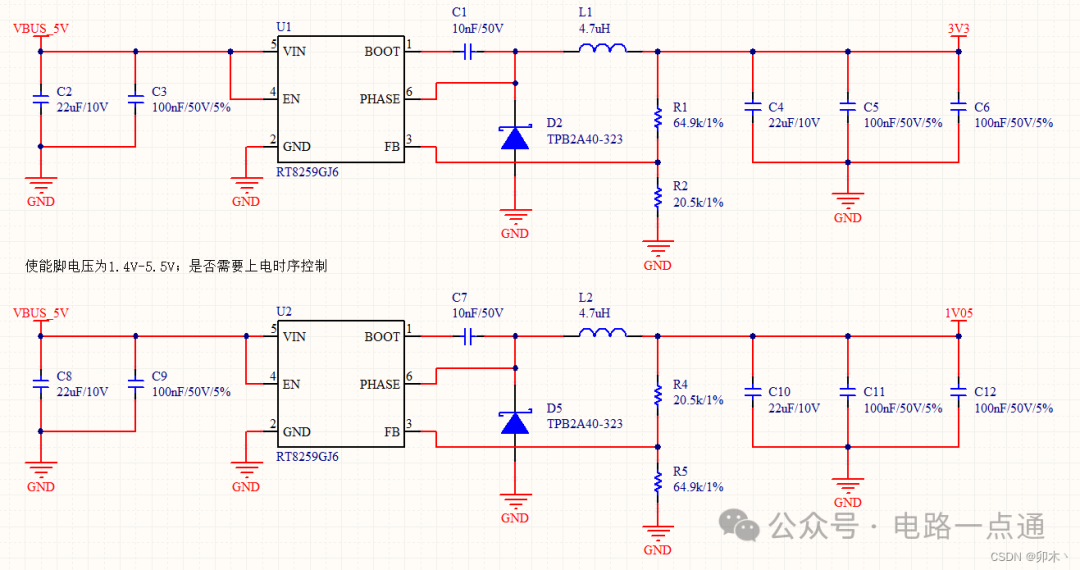
在一块板卡上，存在两个DCDC电源，使用同一块电源芯片RT8259（DataSheet）。电路原理图如图1所示。焊接调试时，发现如下问题：
在空载情况下，3.3V正常输出；1.05V输出在上电初始阶段正常输出，十几秒后会逐渐抬升至1.2V以上，偶尔也会很快抬升至1.2V。
2 测试与解决过程
2.1 问题排除
1、排除原理问题。3.3V能正常输出，说明原理图不存在较大问题；查看手册与原理图，确定芯片正常输出范围为0.8V-15V；
2、排除硬件功能问题。更换反馈电阻，能正常输出3.3V，说明芯片未损坏，电源电路功能正常；
3、排除MOS管导通极限问题。计算电源芯片上端MOS导通时间，
t o n = 1 f S W × V O U T V I N = 150 n s t_{on} = dfrac{1}{f_{SW}} imes dfrac{V_{OUT}}{V_{IN}} = 150ns
t
on
=
f
S
W
1
×
V
I
N
V
O
U
T
=150ns
，大于手册上给出的最小100ns；
2.2 确定问题
测试发现，电源刚上电时，输出与反馈引脚的电压都是正确的。一段时间后，当电源输出抬升
时，FB引脚电压比手册上给出的
0.8 V ( ± 0.016 V ) 0.8V (pm 0.016V)
0.8
V
(±0.016
V
)
要高，达到了
0.85 − 0.95 V 0.85-0.95V
0.85−0.95
V
， 也就是说，反馈网络处于一个不正常的状态。因此，可以推测问题出现在反馈回路上。
查阅手册，其中关于反馈电阻的文字表述仅有关于反馈电压的一个公式
：
V O U T = V F B ( 1 + R 1 R 2 ) V_{OUT}=V_{FB}(1+dfrac{R_1}{R_2})
V
O
U
T
=
V
FB
(1+
R
2
R
1
)
，以及一个电阻推荐选型表。
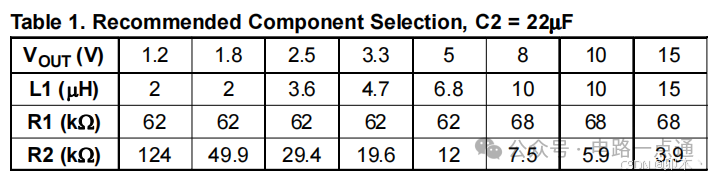根据以往大部分数据手册中会给出的表述，反馈电阻的取值不宜太大。这是因为FB引脚存在一个漏电流
I F B I_{FB}
I
FB
，电源实际输出电压为：
V O U T = V F B ( 1 + R 1 R 2 ) + R 1 × I F B V_{OUT}=V_{FB}(1+dfrac{R_1}{R_2}) + R_1 imes I_{FB}
V
O
U
T
=
V
FB
(1+
R
2
R
1
)+
R
1
×
I
FB
。
I F B I_{FB}
I
FB
在不同器件上以及工作过程中是不断变化的，因此反馈网络阻值太大会导致
I F B I_{FB}
I
FB
在反馈中占比太大，导致输出电压不准确。建议反馈网络电流大于
I F B I_{FB}
I
FB
50倍以上。
同时，反馈网络取值不宜太小，电阻越小，反馈回路的电流和损耗会越大。尤其是功耗敏感的应用中，需要注意反馈电阻带来的损耗。
以上是根据芯片手册和以往经验，在电源设计时考虑的问题。当时，为了统一器件，发现3.3V的反馈电阻，反过来刚好能作为1.05V的反馈分压电阻。本着精简BOM、节约成本的美好品德，直接选用了20.5k+64.9k的电阻（当时还在暗自得意来着）。现在来看，很明显忽略了反馈电阻网络对电源反馈环路带来的影响。查看推荐电阻，可以发现高端电阻
R 1 R_1
R
1
的值，都选在62k以上。增大
R 1 R_1
R
1
的取值到62k以上，重新计算板上的反馈电阻网络。最终调整
R 1 R_1
R
1
为63.4k，低端电阻
R 2 R_2
R
2
为200k，此时电源电压正常输出1.05V。
3 解决问题
查阅手册，增大
R 1 R_1
R
1
的值，解决了板子电源输出不稳定的问题，但并没有解决我的疑问，为什么
R 1 R_1
R
1
太小会导致电源不稳定呢？
3.1 理论分析
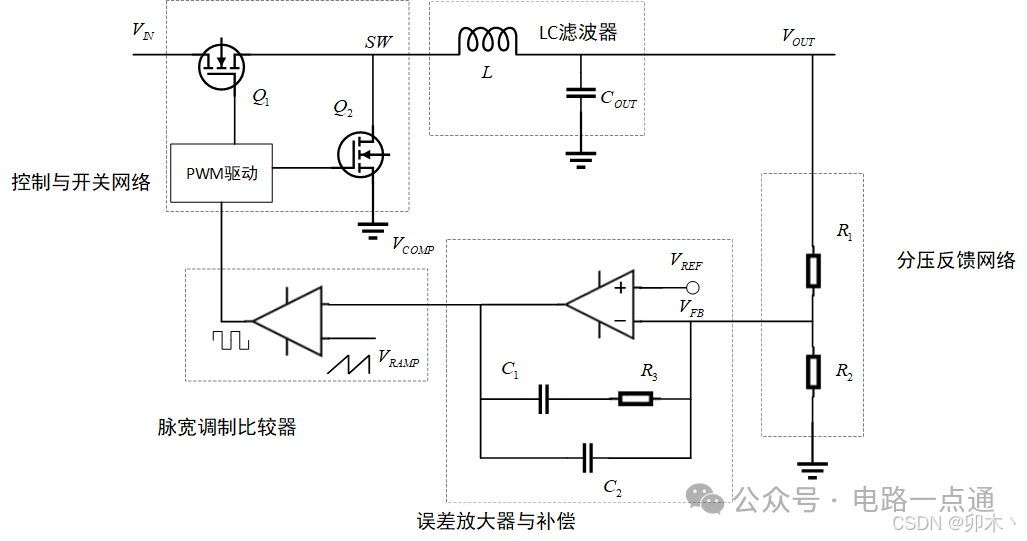
图3所示的是RT8259内部的Buck电路的控制环路，包括脉宽调制比较器、控制与开关网络、LC滤波器、分压反馈与补偿网络。
R 1 R_1
R
1
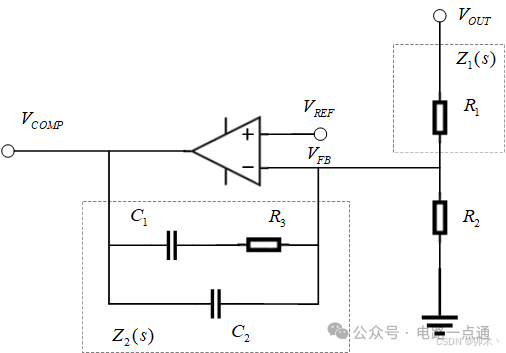
主要影响了其中的分压反馈和误差放大器及其补偿网络。如图4所示，是RT8259内部的电压型II型补偿反馈网络的结构图。依据运算放大器的
虚短
与
虚断
原则，可以推导该反馈网络的传递函数：
当开关电源出现扰动，产生一个小信号
Δ V O U T Delta V_{OUT} Δ
V
O
U
T
时，根据虚短，
V F B V_{FB}
V
FB
的电压会保持与
V R E F V_{REF}
V
REF
相等，也就是
Δ V F B = 0 Delta V_{FB}=0 Δ
V
FB
=0
，根据虚断，变化的电流
Δ I = Δ V O U T Z 1 ( s ) Delta I = dfrac{Delta V_{OUT}}{Z_1(s)}
Δ
I
=
Z
1
(s)
Δ
V
O
U
T
全部经过
Z 2 ( s ) Z_2(s)
Z
2
(s)
流向
V C O M P V_{COMP}
V
COMP
。因此可以得到传递函数：
Δ V O U T Z 1 ( s ) × Z 2 ( s ) = − Δ V C O M P Δ V C O M P Δ V O U T = − Z 2 ( s ) Z 1 ( s ) dfrac{Delta V_{OUT}}{Z_1(s)} imes Z_2(s) = -Delta V_{COMP} \ dfrac {Delta V_{COMP}}{Delta V_{OUT}} = - dfrac{Z_2(s)}{Z_1(s)}
Z
1
(s)
Δ
V
O
U
T
×
Z
2
(s)=−Δ
V
COMP
Δ
V
O
U
T
Δ
V
COMP
=−
Z
1
(s)
Z
2
(s)
将对应的
Z 1 ( s ) Z_1(s)
Z
1
(s)
与
Z 2 ( s ) Z_2(s)
Z
2
(s)
带入：
Δ V C O M P Δ V O U T = − ( R 3 + 1 s C 1 ) × 1 s C 2 R 3 + 1 s C 1 + 1 s C 2 R 1 = − s R 3 C 1 + 1 s R 1 ( s R 3 C 1 C 2 + C 1 + C 2 ) = − 1 R 1 × s R 3 C 1 + 1 s ( s R 3 C 1 C 2 + C 1 + C 2 ) egin{aligned} dfrac {Delta V_{COMP}}{
本站所有转载文章系出于传递更多信息之目的，且明确注明来源，不希望被转载的媒体或个人可与我们联系，我们将立即进行删除处理。
技术咨询
代买器件
商务客服
研发客服
