在本文中，我们将解释方波驱动和正弦波驱动这两种驱动系统如何影响电机扭矩性能。

驱动系统和电机扭矩

与方波驱动系统相比，正弦波驱动系统的转矩波动更小，运行更平稳。

让我们使用电机转矩产生的原理来考虑其原因。如图 2.2 所示，电机的理想驱动方法是根据弗莱明左手定则，使磁通量和线圈电流始终正交。这种驱动方法适用于所有电机类型。在直流有刷电机中，这是通过机械换向完成的。为了解释无刷电机转矩产生的原理，我们将使用一个简化的三相 2 极模型，如图 3.4 所示。

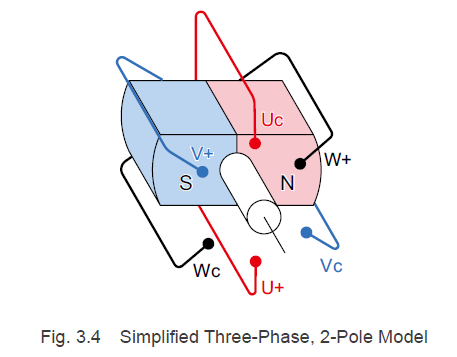
转子在北极和南极之间的中心包含一个旋转轴。在围绕转子磁体的定子中，U 相、V 相和 W 相线圈绕组彼此偏移 120°。

U+、V+、W+接驱动电路，Uc、Vc、Wc接在一处(公共端)。在这里，我们将从驱动电路流向公共端的方向指定为“正”，将从公共端流向驱动电路的方向指定为“负”。

让我们详细了解特定相的线圈。从图 3.5 中线圈和转子磁铁的状态可以看出，转子和定子的位置与它们在直流有刷电机中的位置相反。如果电流流过该点，如图3.5所示，南极侧会产生向下的电磁力，北极侧会产生向上的电磁力，由弗莱明左手定则确定. 然而，由于无刷电机中的线圈是固定的，因此作用在转子磁铁上的反作用力会使转子顺时针转动。

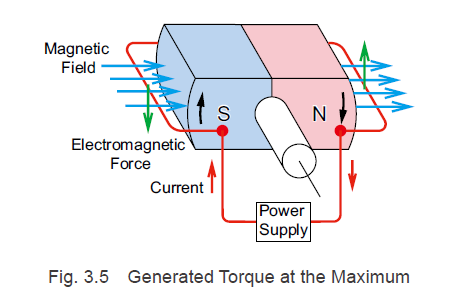
在图 3.5 所示的状态下作用于绕组的电磁力F [N] 可使用在 DC 电机旋转原理部分中说明的以下公式计算得出。

然而，如果转子旋转并呈现图 3.6 所示的状态，则作用在导体上的电磁力F会在线圈向外侧延伸的方向上产生，因此不会产生朝向转子的力(扭矩)旋转部分的磁铁。

换言之，对于导体而言，作为转矩起作用的磁通密度B的方向与旋转轴正交并且根据转子磁体的旋转角度而变化。

当转子旋转时，假设作为扭矩作用于彼此偏移 120° 的 U 相、V 相和 W 相线圈的磁通密度变为正弦曲线形式。

图3.4所示转子转角为0°、最大磁通密度为B0顺时针旋转时，转子转角与各相磁通密度的关系，分别表示为Bw、Bv、Bw，由式(3.2)表示。

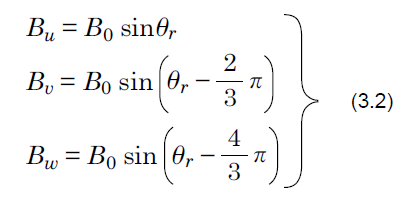
3.2.1 对于方波驱动系统

为了解释使用方波驱动时的电机扭矩，我们将使用简化的三相 2 极模型，如图 3.4 所示。

驱动电流

对于方波驱动系统的无刷电机，如“2.2.2 无刷电机旋转原理”中所述，电流根据转子角度的励磁模式流向 U 相、V 相和 W 相的线圈由磁极传感器检测。

如果顺时针旋转，图 3.4 所示的转子角度为 0°，电机电流为i m，则转子角度与各相的相电流之间的关系如图 3.8 所示。

此时，当转子转角在30°和150°之间时，流过U相的电流为im，在210°和330°之间为-im。相对于 U 相电流，V 相和 W 相的电流分别经历 120° 和 240° 的相位延迟。

电机扭矩

使用电磁力 F 和从转子旋转中心到导体的距离 r 计算每个相线圈产生的转矩 T。

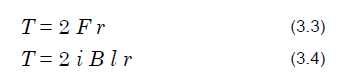
因此，电机转矩是各相线圈产生的转矩之和，用下式表示。

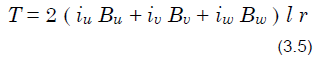
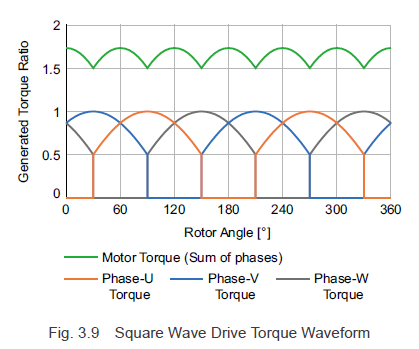
如果将r、l、 im和B0设置为 1，并且使用公式(3.2)、图 3.8 和公式(3.5)根据每个转子角度的电流和磁通密度计算每相转矩，则结果是图 3.9 所示的扭矩波形。因为每转产生6个转矩脉动，所以在低速旋转时会产生速度脉动。

3.2.2 对于正弦波驱动系统

为了解释使用正弦波驱动时的电机扭矩，我们将使用简化的三相 2 极模型，如图 3.4 所示。

驱动电流

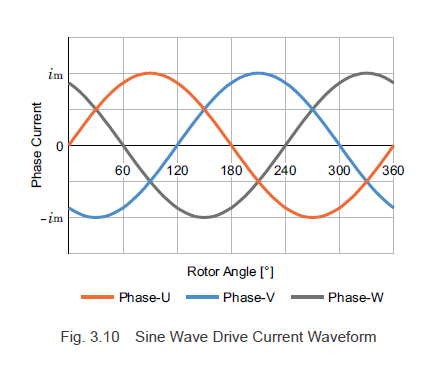
当转子顺时针旋转时，相位差为 120° 的正弦电流如图 3.10 所示，流向 U 相、V 相和 W 相的线圈，它们与相差 120°另一个。在图 3.4 中，若顺时针旋转，转子转角为 0°，电流最大值为im，则各相电流分别记为iw1、iv1和iw1，如式(3.6)所示。

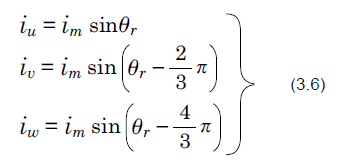
电机扭矩

与方波驱动一样，电机转矩是各相线圈产生的转矩之和，使用公式(3.5)计算。

此外，公式(3.5)可以使用公式(3.2)和公式(3.6)简化如下所示。

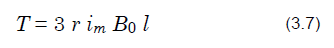
设式(3.7)中的r、l、im、Bo为1，计算各转子转角各相电流与磁通密度的乘积之和，则转矩波形如图. 3.11. 式(3.7)中，转子角θ项消失，图3.11中电机转矩为常数。换言之，采用正弦波驱动，任何旋转都没有转矩脉动，低速旋转时也可以平稳运行。

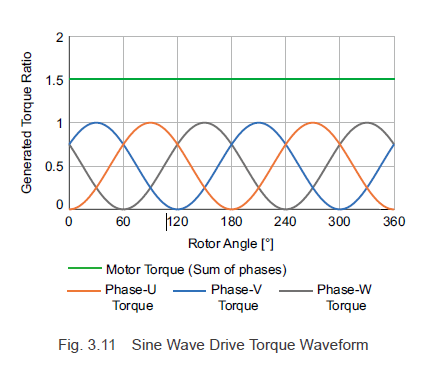
为了获得最佳性能，Oriental Motor 的无刷电机驱动器采用正弦波驱动方法。