在本文中，我们探讨了两种不同的方法来分析传输线变压器的阻抗变比。

通过使用传输线代替绕组，传输线变压器能够在高频和宽带宽下运行。正如我们在前面的文章中所了解的那样，这些功能使得它们在射频和微波应用中非常有用。然而，初学者常常发现传输线变压器难以进行分析。

在本文中，我们将逐一介绍传输线变压器分析的两种常见方法，试图消除一些困惑。我们将要检查的第一种方法——文章标题中的“困难方法”——以花更多的时间做数学为代价，提供了更高水平的准确度。第二种方法提供了一个简单的分析，通常但并不总是足够的。在采取简单的方法之前，了解困难的方法是很重要的。

难点：使用传输线方程式

传输线变压器依靠电磁波通过传输线传输能量至输出。因此，应考虑传输线方程式进行严格分析。例如，图1显示了一个采用双极线圈构建的反相器电路。

采用双线圈构建的宽频带变频器示意图。

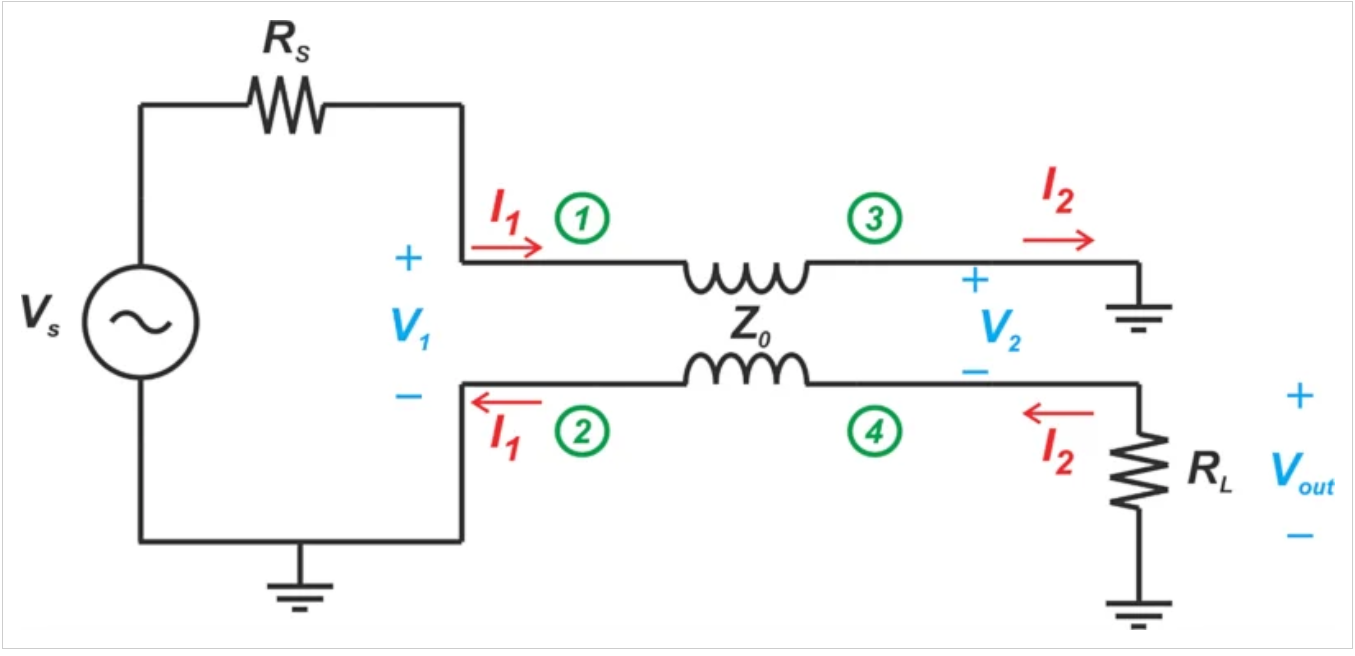
•图1。一种宽频带双线圈移相器。

为了分析这个电路，我们将使用传输线的ABCD参数来描述传输线的输入端口和输出端口之间的关系。考虑图2中的无损传输线，其特征阻抗为Z0，相位常数为β，长度为l。

无损传输线。

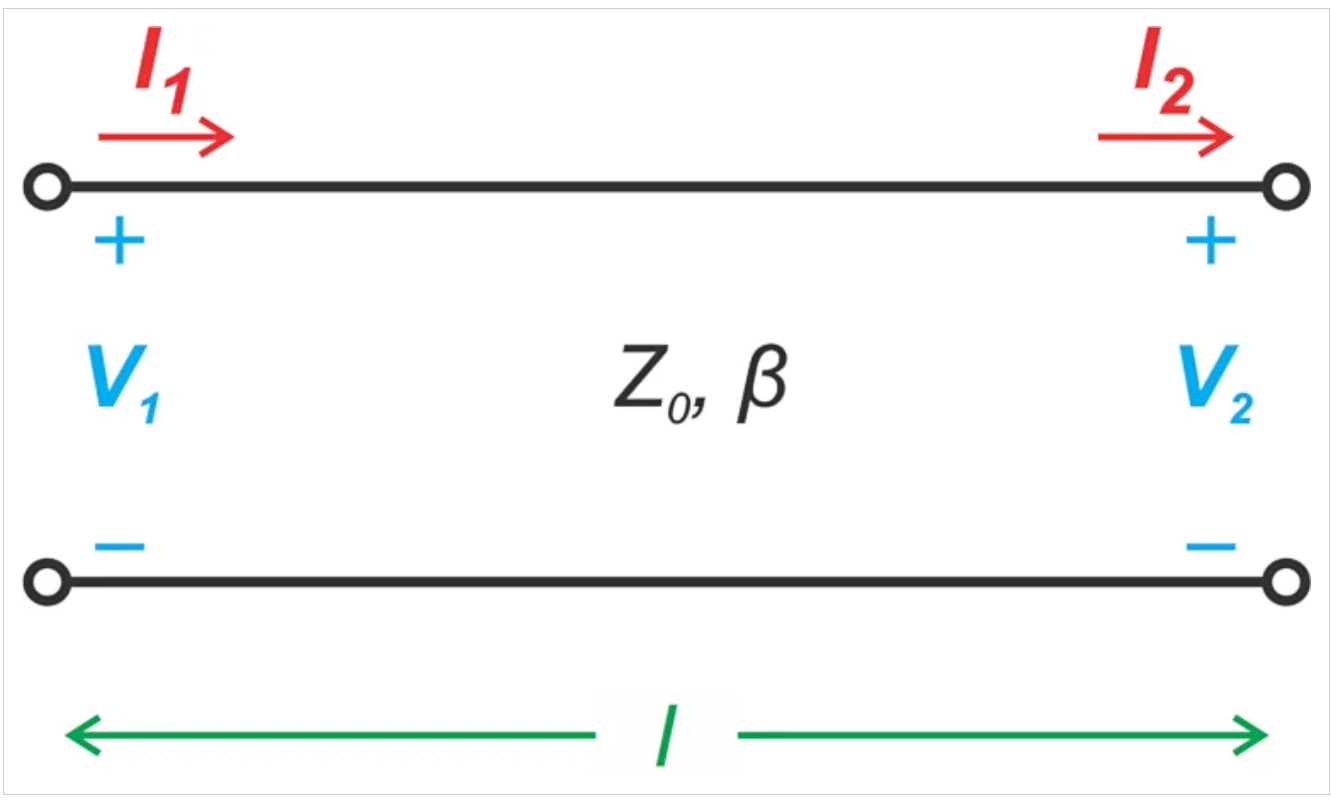•图2。具有特性阻抗Z0、相位常数β和长度l的传输线。

传输线的ABCD表示通过以下方程式描述输入端口和输出端口的电压和电流量：

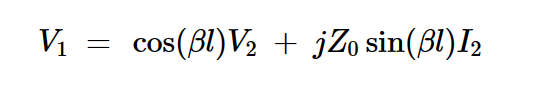
•方程式1。

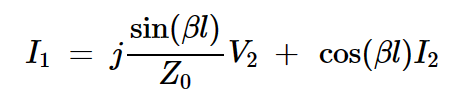
•方程式2。

我们将使用这两个主要方程式来分析反相器电路。我们还将从图1中获得一个额外的方程式，以关联输出电压和电流：

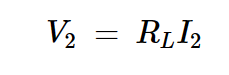
•方程式3。

假设匹配负载（Z0=RL），我们可以使用一些代数将方程式3与方程式1结合起来。这给出了输入和输出电压之间的关系：

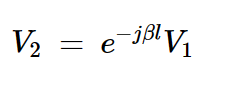
•方程式4。

如该方程式所示，对于匹配负载，沿着传输线的信号振幅是恒定的。该线仅向输入信号引入相移。

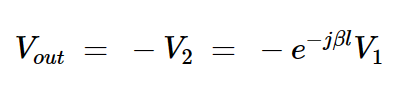
•方程式5。

这表明，如果指数项的相移可忽略不计，则电路起到了反相器的作用。对于要呈现180度相移的传递函数，我们应该具有 βl ≪ 1。回想一下，相位常数β由下式给出：

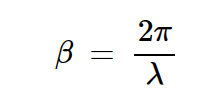
•方程式6。

因此，为了忽略指数项的相移，线的长度应满足以下约束条件：

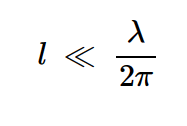
•方程式7。

总之，要使电路起到反相器的作用，必须满足两个条件：

线路损耗必须可忽略不计。

线的长度必须足够短，以便忽略指数项的相移。

这种方法虽然精确，但相对数学密集。让我们讨论一个更直观的方法来确定电路的阻抗变比。

简单方法：集中电感法

当分析阻抗变换时，许多书都认为传输线变压器的性能与磁耦合变压器相似。这个假设让我们能够避免我们在前面的小节中看到的复杂的数学。例如，让我们来看一下，如果我们分析图3中产生的反相器电路以便于参考，就像它是一个磁耦合变压器一样，会发生什么。

一种宽带反相器，由双线圈构成，但被分析为磁耦合变压器。

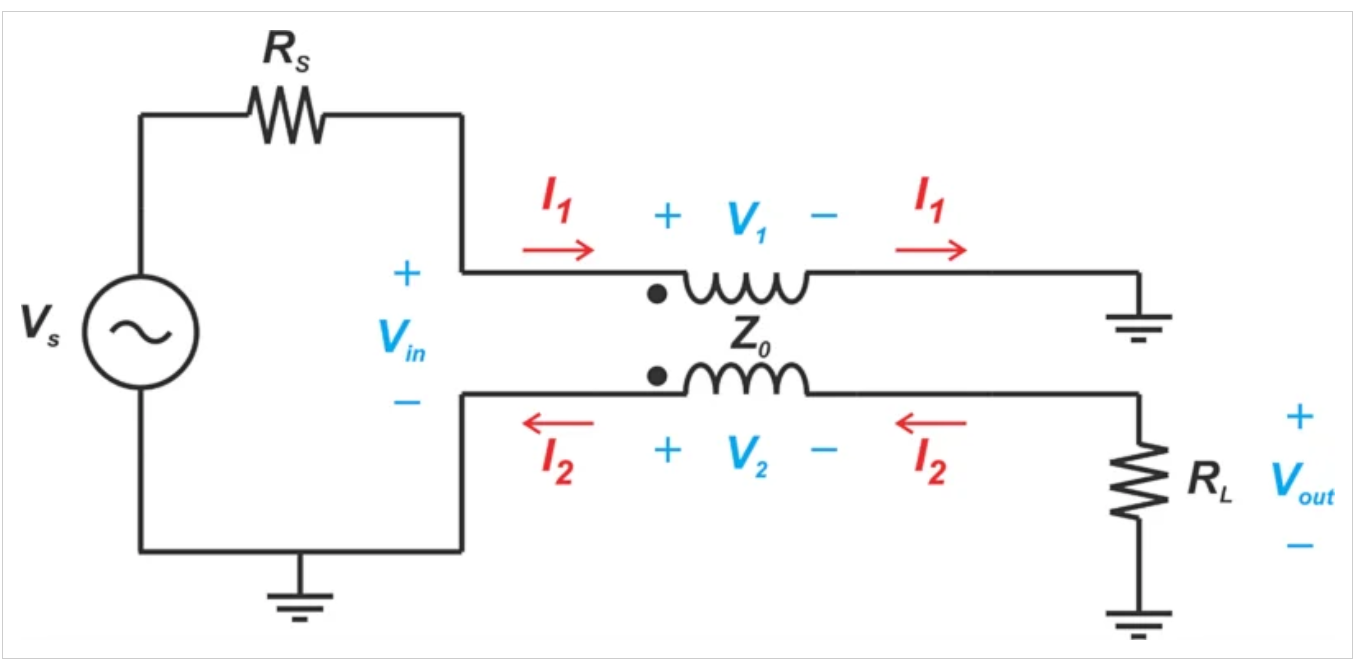
•图3。将宽带变频器作为传统变压器进行分析。

在这种情况下，我们假设初级绕组（V1）两端的电压也施加在次级绕组（V1=V2）两端。同样，相同的电流流过一次和二次绕组。为了找到电压的极性和电流的方向，我们将变压器点约定应用于上图。应用基尔霍夫电压定律，我们得出：

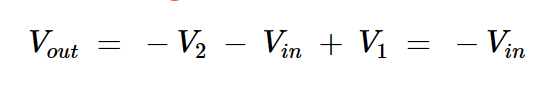
•方程式8。

这与我们之前进行的更精确的数学分析一致。

当正确应用时，简化的方法将提供与更严格的分析相同的阻抗变换比。因此，许多参考文献仅给出了简化分析。然而，这种方法依赖于我们对电路的行为做出某些假设，特别是，离开绕组的电流与进入绕组的电流相同。

这是我们使用集总电感的分析类型。我们假设传输线变压器的绕组充当集总电感器，以下两种说法必须正确：

电路工作频率较低。

传输线相对波长较短。

由于传输线变压器可在相当大的频率范围内充当磁耦合变压器，所以只要满足上述两个条件，简化分析是有效的。然而，在高频下，我们应该使用传输线方程式来获得对电路行为的全面了解。传输线分析假设绕组充当分布式元件，导致进入绕组的电流与离开另一端的电流不同。

下一篇

在本文中，我们学习了分析传输线变压器的两种不同方法。本系列的未来文章将使用这些知识——我们将使用本文介绍的两种分析技术来研究Ruthroff类变压器。在此之前，我希望你们已经发现今天的讨论内容丰富。