频域法是在图像的频率变化域中对图像的变换值进行某种运算处理，然后再变回空间域中。

一、频域图像增强的原理

二、低通滤波器

1.理想低通滤波器

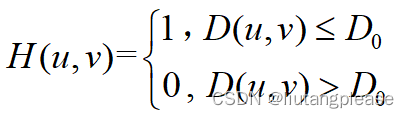
2.巴特沃斯低通滤波器

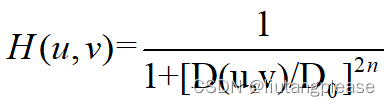
滤除高频分量（>90%），去除噪声的同时易丢失图像的细节信息

三、高通滤波器

1.理想高通滤波器

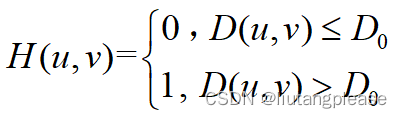
2.巴特沃斯高通滤波器

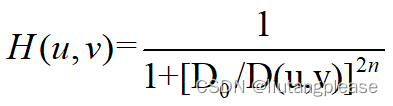
突出高频的同时不损害图像的低频部分，使图像不会模糊

四、带通与带阻滤波

1.带阻滤波器

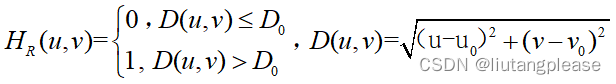
2.带通滤波器

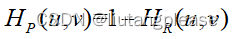
五、同态滤波

同态滤波是一种在频域中同时将图像亮度范围进行压缩和将图像对比度进行增强的方法。

六、上述滤波器的MATLAB实现

F=fft2(f);   %对图像进行傅立叶变换

S=fftshift(log(1+abs(F)));   %对变换后图像进行对数变化，并对其坐标平移，使其中心化

h=fspecial('sobel'); %产生空间‘sobel’模板

H=freqz2(h,f(1),f(2)); %产生频域中的‘sobel’滤波器

AAA=imnoise(A,‘salt & pepper’,0.25);%加椒盐噪声

d0=50; %阈值

img_noise=imnoise(img_origin,'salt'); % 加椒盐噪声img_noise=imnoise(img_origin,'gaussian'); % 加高斯噪声img_f=fftshift(fft2(img_noise)); %傅里叶变换得到频谱

[m n]=size(img_f);

m_mid=fix(m/2); %取整

n_mid=fix(n/2); img_lpf=zeros(m,n);

for i=1:m  

   for j=1:n    

     d=sqrt((i-m_mid)^2+(j-n_mid)^2);  %理想低通滤波，求距离    

      if d<=d0            h(i,j)=1;      

           else            h(i,j)=0;        

           end      

     img_lpf(i,j)=h(i,j)*img_f(i,j);    

     end

end

img_lpf=ifftshift(img_lpf);    %反傅里叶变换

img_lpf=uint8(real(ifft2(img_lpf)));  %取实数部分

subplot(2,2,1);imshow(ggray);title('原图');

subplot(2,2,2);imshow(img_noise);title('噪声图');

subplot(2,2,3);imshow(img_lpf);title('理想低通滤波');