脉宽调制（或简称PWM）是一个简单的概念，有许多应用。我们来看一个方波。

　　　波形有一定的频率。波形的频率和周期彼此相反，即频率= 1/周期，周期= 1/频率。1s的周期意味着1Hz的频率。0.1s的周期表示10Hz的频率，10s的周期表示0.1Hz的频率

　　请注意，该信号完全是数字信号，要么为开/高电平，要么为关/低电平。例如，这不同于正弦波，正弦波是模拟的，在整个波形中平滑过渡（参见我们关于模拟和数字信号的文章）。

　　还要注意的是，对于方波，信号在一半时间内是开启的，在一半时间内是关闭的。

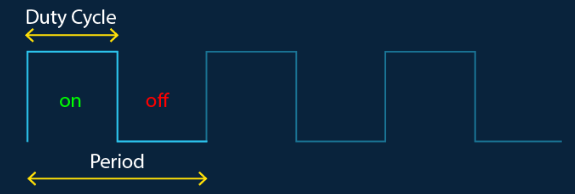
　　波形的on部分称为占空比——它是信号供电/做功/工作的时间比例。对于方波，这是50%的时间，意味着信号有50%的占空比；即，如果周期为1s（频率为1Hz），则信号将开启0.5s，关闭0.5s

　　波形的正部分也可以被认为是一个能量脉冲。通过修改脉冲的宽度（占空比），我们可以改变波形中能量的比例。

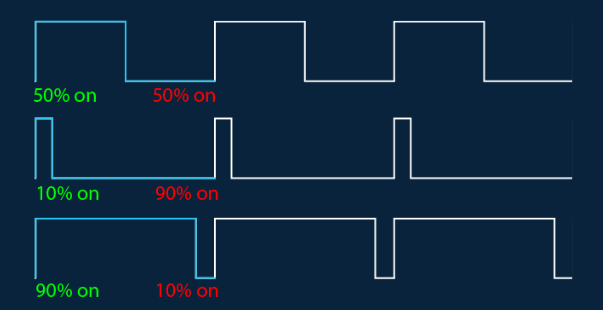
　　　由此而来的术语脉宽调制（修改脉冲的宽度）。

　　PWM的主要用途

　　脉宽调制（以下简称为PWM）是数字系统产生模拟输出的一种方式（通过将PWM信号通过一些附加电路和/或机械系统）。PWM的一些应用示例如下：

　　PWM信号可用于通过低通滤波器产生模拟电压。

　　PWM可用于按比例控制DC电机的速度。

　　PWM用于设置某些类型的伺服电机的位置。

　　PWM可用于控制加热元件产生的热量。

　　PWM用于降压和升压转换器，将输入电压向下转换为较低电压或向上转换为较高电压（参见我们的巴克和升压转换器文章）。

　　PWM可用于控制灯泡或LED的［表观］亮度。

　　。。.还有很多很多。

　　在某些情况下，输出是电压或电流，在其他情况下，它是物理量，如力/位置/热量/亮度，但在所有情况下，通过使用PWM，输出可以在完全打开的最大值和完全关闭的最小值之间平滑缩放。

　　PWM到模拟信号

　　让我们看看将PWM信号转换为模拟电压的情况。为此，我们需要一个低通滤波器（参见我们的过滤文章）。

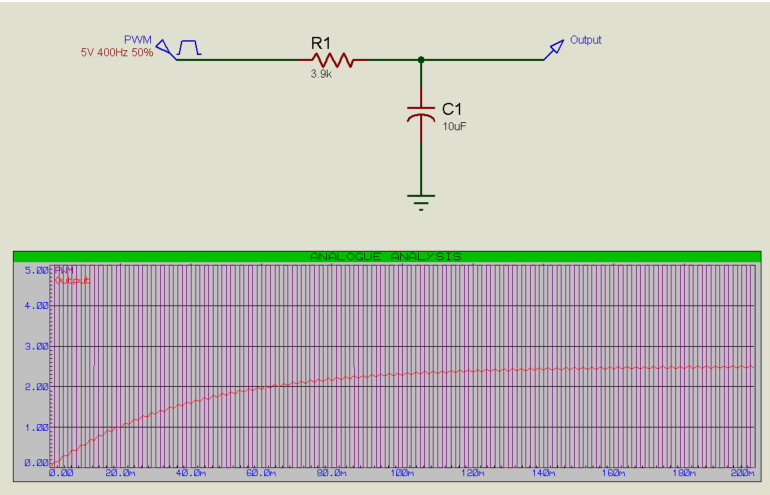
　　5V数字PWM转换为2.5V模拟输出（5V的50% = 2.5V）。

　　R（电阻）或C（电容）值越小，对输入变化的响应越快，但输出抖动越大（反之亦然）。

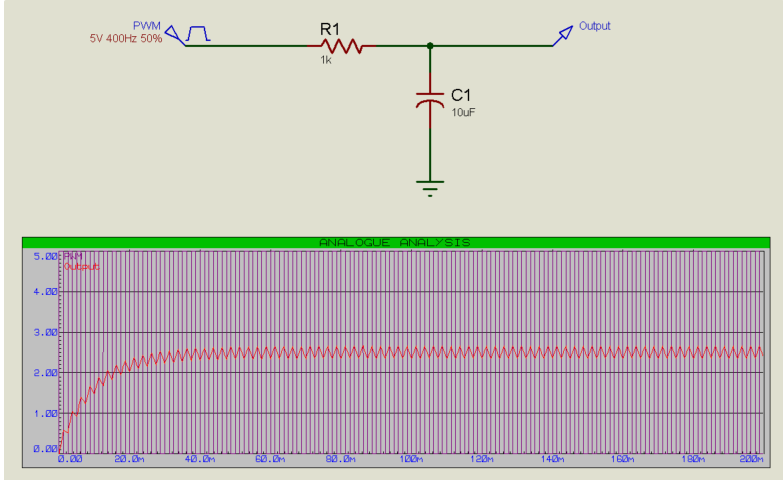
　　改变占空比会改变输出电压。例如，20%的占空比将产生1V的输出（5V的5V = 1V）：

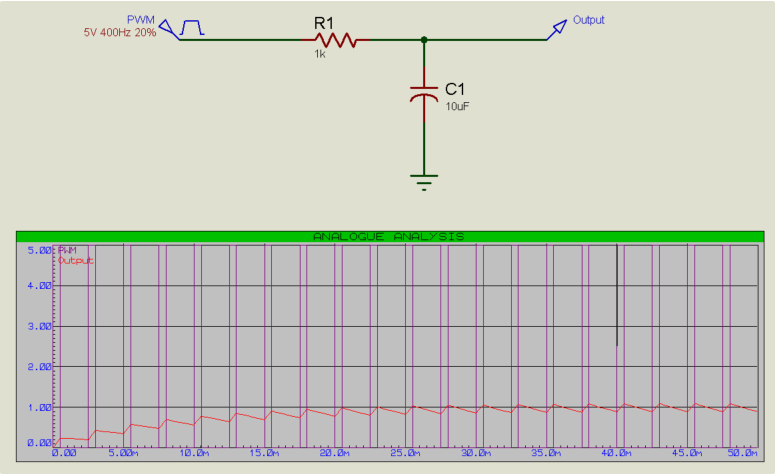
　　相反，80%的占空比将产生4V的输出（80%的5V = 4V）：

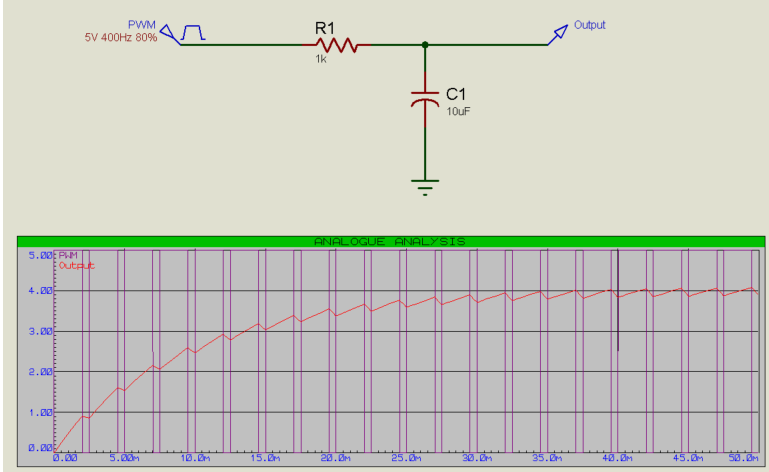
　　提高PWM的频率也会降低输出的抖动：

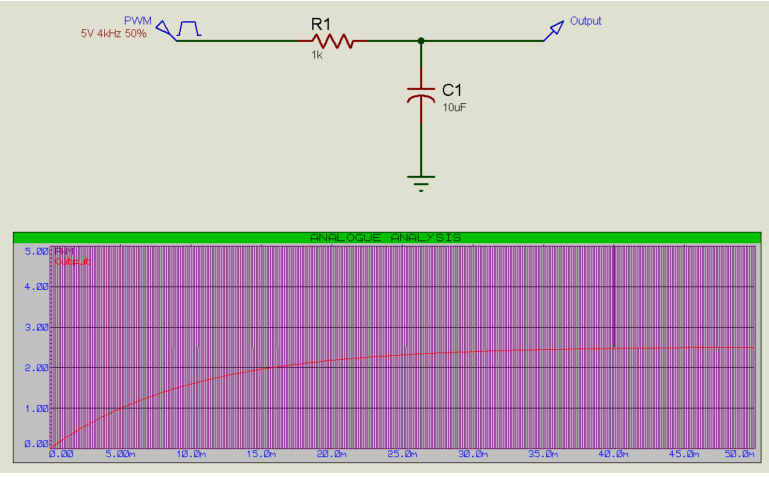
　　请注意，这反过来意味着可以使用相对较低的电阻和/或电容值，因此对输入变化的响应相对较快。这是PWM的一般规则：PWM频率越高，输出越平滑，响应越快。

　　然而，关于响应度，请记住，为了提高响应度，系统中的平滑元件（上例中的电阻电容低通滤波器）必须做得更小。或者，应该增加输入功率电平（上面例子中的输入波形电压）。在一个机械系统中，系统的平滑元素可能是系统的惯性（质量）——后面会详细介绍。

　　PWM频率的上限总是存在的——这可能受到产生PWM的数字系统的时钟频率的限制，或者受到输出系统中开关元件响应速度的限制——例如，一个继电器可能需要几毫秒来切换，或者一个阀门可能需要一些时间来打开/关闭。

　　正如我们的无源滤波器文章中，也可以使用电感-电阻低通滤波器：

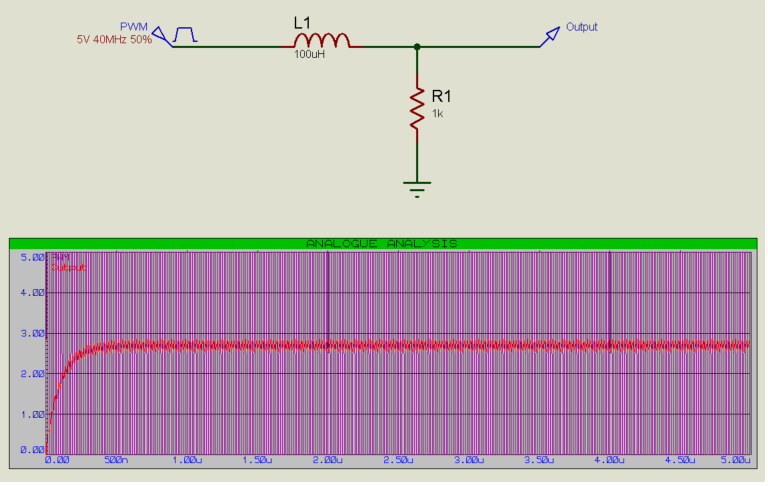
　　然而，由于所需的频率/元件尺寸较低，阻容滤波器通常更适合这种特殊应用。

　　嵌入式PWM

　　大多数现代微控制器都内置PWM外设，可以在一定的频率和分辨率范围内产生PWM输出。如果需要的频率低于PWM外设所能产生的频率，那么可以使用定时器中断并手动将引脚设置为高电平和低电平。

　　在Arduino中，analogWrite（）函数直接生成PWM输出：

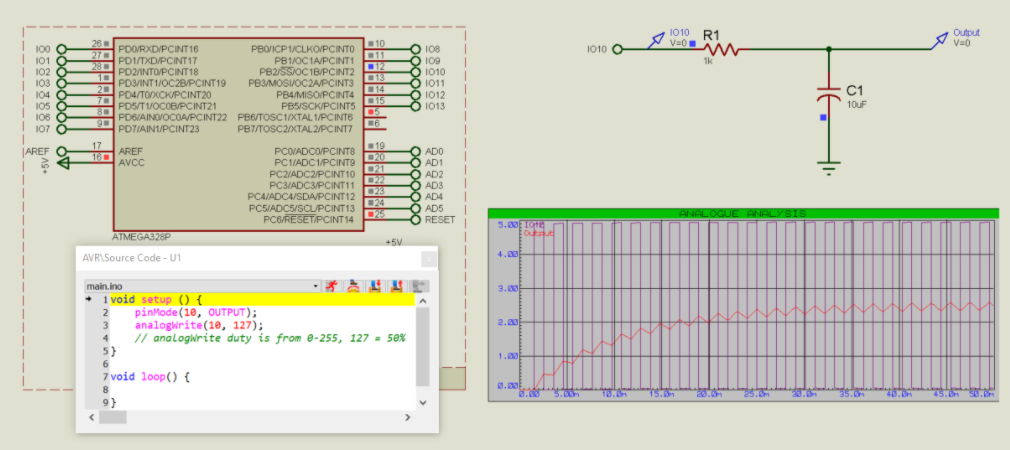
　　带机械元件的PWM

　　对于机械系统，系统的平滑元素通常是系统的惯性，即系统对输入变化的反应速度。这包括在我们的巴克和升压转换器使用飞轮/旋转木马概念的文章。

　　想象一下，我们在旋转木马上加了一个喷水器，我们可以用一个电磁阀打开和关闭这个喷水器。

　　如果我们打开阀门，那么旋转木马会转得更快，如果我们关闭阀门，那么旋转木马会由于空气和轴承的阻力而自然地慢下来。

　　根据牛顿第二运动定律，加速度=力/质量。如果我们假设力是恒定的（对于PWM，力通常被假设为恒定的，因为波形的电压是恒定的——我们现在不会变得比这更复杂，我们将假设水压是恒定的），那么我们可以看到加速度完全取决于质量（惯性）。旋转木马旋转的速度将由公式速度=加速度x时间给出。从这些公式中我们可以看出，速度与力成正比，如果力只施加了50%的时间（50%的占空比），那么速度也将是持续施加力时的50%。10%的占空比意味着10%的速度，90%的占空比意味着90%的速度，以此类推。由此可见，我们可以通过改变占空比，从数字输入（控制水射流完全打开或完全关闭）产生模拟输出（速度）。

　　有一些方面我们还没有详细研究，例如作用在水射流相反方向的阻力的细节，以及水射流与中心的距离将如何影响事物，但是我们已经研究的内容足以涵盖PWM原理。我们可以注意到，PWM的最大频率将受到控制喷水器的螺线管打开和关闭速度的限制，并且系统中的抖动（对于给定的频率）将取决于旋转木马的质量——这是因为旋转木马总是在加速（喷水器打开）或减速（空气/轴承阻力），但是质量越高，这些力产生的加速度（速度变化）越小（抖动越小）。

　　同样的原理也适用于由磁场驱动的DC发动机（而不是喷水器）、水箱中的加热元件、DC灯泡等等。PWM导致的LED明显变暗是由于我们眼睛的光学帧率（视觉暂留），但这是另一篇文章的主题！

　　总体而言，PWM的原理非常简单——将数字输入转换为模拟输出。系统中的变量是平滑元件的力（电压）、频率、占空比和惯性；并且这些的调谐限制因应用而异。