了解可用功率增益概念如何帮助我们解决为指定增益和噪声系数设计双边RF放大器的问题。

在设计低（LNA）时，我们需要考虑增益和噪声性能。正如我们在上一篇文章中所了解的，我们可以使用RF晶体管的恒定噪声系数（NF）轮廓来确定给定噪声性能的适当源端接。恒定NF轮廓在ΓS平面中绘制；为了设计噪声和增益放大器，我们需要在ΓS平面中绘制晶体管的增益轮廓。

我们已经介绍了在单边设备的情况下如何实现这一点，其中输入和输出匹配网络的增益是相互独立的。本文探讨了针对特定增益和噪声系数的双边LNA的设计，这可能有点复杂。

为了设计一个指定增益而非最大增益的双边放大器，我们可以使用工作功率增益（GP）或可用功率增益（GA）。然而，恒定GP圆在ΓL平面中绘制，因此它们不能直接用于分析放大器的增益噪声权衡。另一方面，恒定GA圆在ΓS平面中指定。因此，我们将使用可用功率增益概念来设计我们的双边LNA。

可用功率增益

可用功率增益（GA）是网络可用功率（PAVN）与源可用功率（PAVS）的比率：

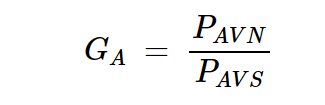
方程式1

图1说明了如何确定模块的可用功率增益。

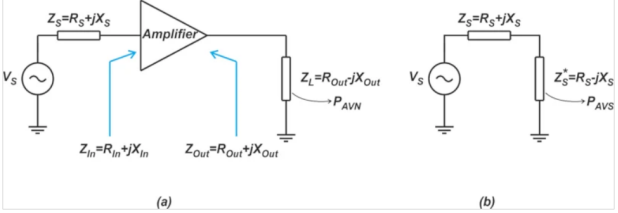
图1.确定放大器的可用功率增益（a）和源的最大可用功率（b）。

在GA方程中，PAVN被归一化为源的可用功率，因此我们对此功率增益测量的参考点是输入电压源（VS）。随着射频功率从源传输到放大器输出，它受到晶体管输入（ZS和ZIN）阻抗失配的影响。因此，PAVN取决于源端接（ΓS）。

然而，如图1(a)所示，我们将模块输出连接到共轭匹配负载以测量PAVN。这就是为什么PAVN不依赖于我们最终连接到放大器的负载终端（ΓL）。我们可以通过检查以下可用功率增益方程来验证这一点：

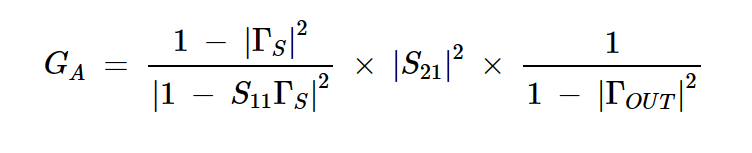
方程式2

其中，在晶体管输出端看到的反射系数ΓOUT由下式给出：

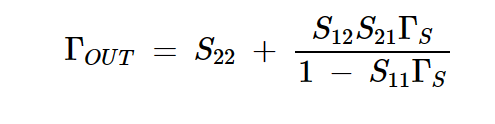
方程式3

请注意，GA不是ΓL的函数，而是ΓS的函数。

在放大器设计中使用可用功率增益

由于方程2只是ΓS和S参数的函数，我们可以使用它来为给定的GA找到合适的ΓS。但这能完全解决我们的设计问题吗？放大器实际呈现的增益是其传感器增益，它由ΓS和ΓL组成。传感器增益由下式给出：

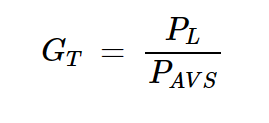
方程式4

如果我们想使用其可用功率增益设计放大器，我们需要找到GA和GT之间的关系。比较方程1和4，我们看到，如果我们有 PL = PAVN，这两个功率增益变得相同。因此，如果我们将ΓL等于Γ*OUT，我们将有GA = GT。

总之，为了通过可用功率增益概念设计特定增益，我们使用方程式2来找到产生所需GA的ΓS值，然后在输出端提供共轭匹配，使器件实际增益GT等于所选GA。

无条件稳定装置的设计方程

现在我们了解了总体设计过程，让我们来看看无条件稳定装置所需的方程。产生给定GA的ΓS值位于恒定GA圆上。该圆的中心（cA）由下式给出：

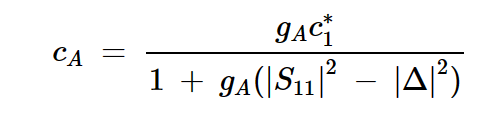
方程式5

其半径（rA）由下式计算：

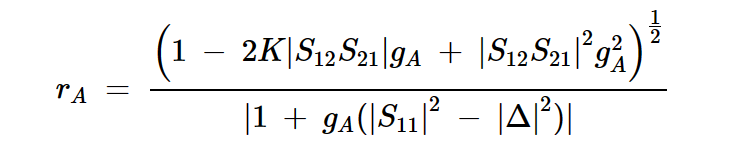
方程式6

上述方程中的参数gA和c1分别由以下公式定义：

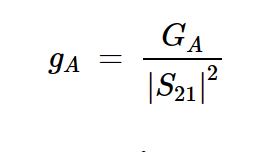
方程式7

以及：

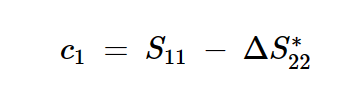
方程式8

K是Rollet的稳定系数：

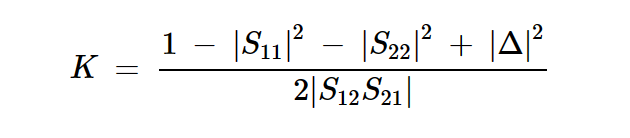
方程式9

Δ是S参数矩阵的行列式：

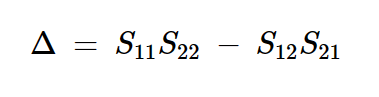
方程式10

对于无条件稳定的装置，GA的最大值由下式给出：

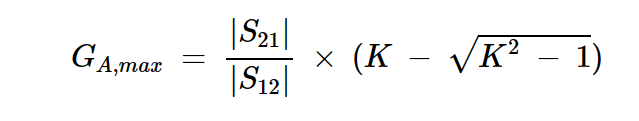
方程式11

另外，GA,max的方程式也是 GP,max和GT,max的方程式。

示例 1：绘制射频晶体管的 GA 圆

现在我们有了必要的方程，我们将通过一些例子来学习。首先，让我们绘制一些恒定GA圆，用于表1中f=1.4GHz的晶体管S参数。

表1.示例晶体管的S参数。Z0=50Ω。

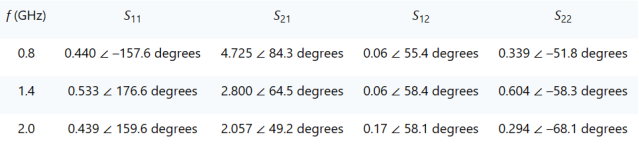
正确地说，我们应该验证该设备在上述三个频率上都是无条件稳定的。但为了简洁起见，我只包括针对f = 1.4 GHz的K系数测试。

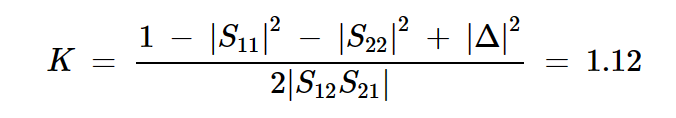
方程式12

由于K大于1且|Δ|<1，因此该器件在所选频率下是无条件稳定的。因此，我们可以使用上述设计过程来找到合适的源端和负载端。首先，应用方程11，我们找到GA的最大值：

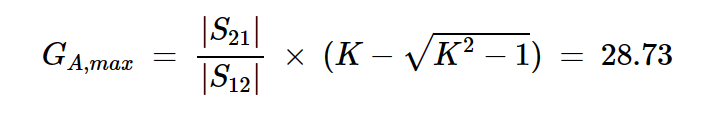
方程式13

这转化为GA，max = 14.58 dB。

我任意选择了GA = 11 dB、12 dB、13 dB和14 dB的恒定增益圆。使用上述数据和方程，我们知道以下内容：

|S21|2=7.84

K=1.12

Δ=0.16，∠=113.32度

c1=0.44，∠177.66度。

因此，我们可以应用方程式5和6来计算恒定GA圆的中心和半径。表2提供了计算总结。

请注意，将GA从dB转换为线性项是我们必须做的第一组计算。我们需要使用方程7来确定gA，然后才能计算cA或rA，方程7要求GA为线性项。

表2.绘制示例晶体管恒定GA圆所需计算总结。

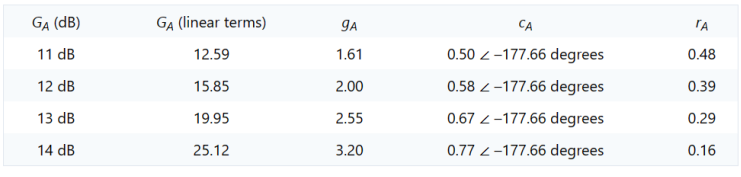
这些恒定的GA圆圈绘制在图2中。

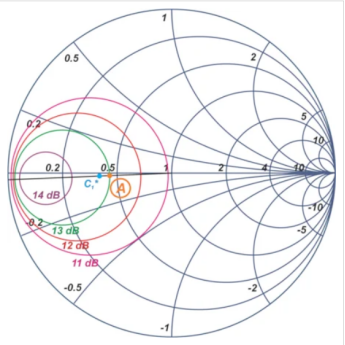
图2:示例晶体管的恒定GA循环，GA=11dB（粉红色圆圈）、12dB（红色圆圈）、13dB（绿色圆圈）和14dB（紫色圆圈）。

恒定GA圆的中心始终位于连接c*1和原点的直线上。要找到原点，请参见方程式5。

示例2：为特定增益设计具有完美匹配输出的放大器

让我们使用前一个示例中的晶体管设计一个在f=1.4 GHz时增益为13 dB的放大器，并确保我们在这样做时晶体管的输出端完美匹配。

由于我们希望在输出端实现完美匹配，我们将使用可用的功率增益方法。图2中绿色常量GA圆上的任何源端接法都可以用来实现13 dB的可用增益——我任意选择了ΓS = 0.38 ∠ –177.66度，标记为上图中的点A。在确定了ΓS后，我们可以找到晶体管输出端的反射系数：

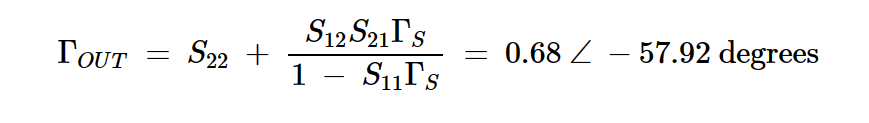
方程式14

现在我们只需要在输出端提供复共轭匹配，使GT = GA = 13 dB：

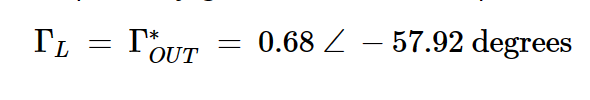
方程式15

这种ΓL的选择也确保了输出端的完美匹配（VSWR=1）。

如果我们将ΓS = 0.38 ∠ –177.66 度 和 ΓL = 0.68 ∠ 57.92 度 代入传感器增益方程，我们得到：

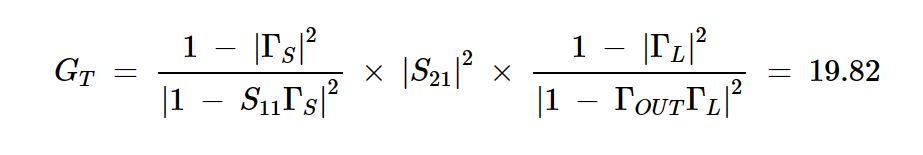
方程式16

从线性项转换，这变为12.97 dB。这与GT = 13 dB的目标值非常接近。

我们现在可以使用Z Smith图来设计输入和输出匹配网络。要设计输入匹配网络，我们首先在Smith图上定位ΓS，并通过沿恒定|ΓS|圆旋转180度找到其关联的归一化导纳（yS）（图3）。

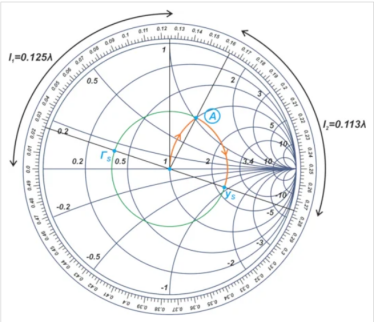
图3. 示例射频放大器输入匹配网络设计的。

从现在开始，我们将解释为Y史密斯圆图。我们想要一个电路，从圆图的中心（50Ω终端）到yS。恒定值|ΓS|圆与1 + jb圆的交点，标记为点A，其电纳为j0.84。

为了产生j0.84的电纳，我们在50Ω终端上添加长度为l1=0.109λ的并联开路短截线。然后添加长度为l2=0.091λ的串联线路，沿着恒定的|ΓS|圆到yS。这解决了输入匹配部分的问题；输出匹配部分可以以类似的方式设计，如图4所示。

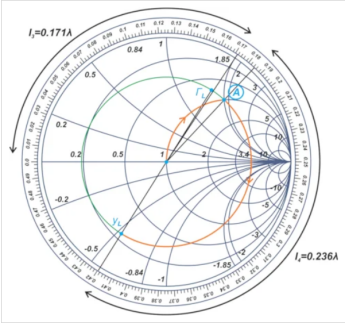
图4. 示例放大器输出匹配网络设计的史密斯圆图。

我们可以看到，输出匹配网络需要长度为l3 = 0.171λ的开路短截线，以及长度为 l4 = 0.236λ.的串联线。

图5显示了最终设计的交流原理图，包括输入和输出匹配网络。

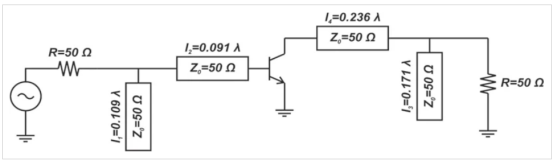
图5.我们示例放大器的最终设计。

图6显示了放大器的模拟增益，非常接近期望值GT = 13 dB。

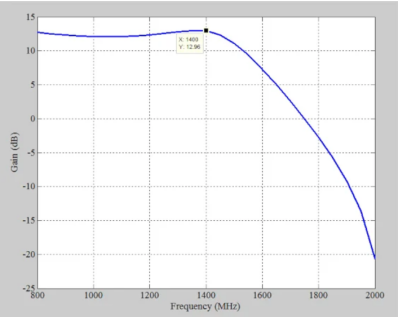
图6.我们设计的放大器的模拟增益。在1400 MHz时，增益为12.96 dB。

图7显示了放大器的输入和输出反射系数。从图中可以看出，使用可用的功率增益方法可以产生输出匹配良好而输入不匹配的放大器。

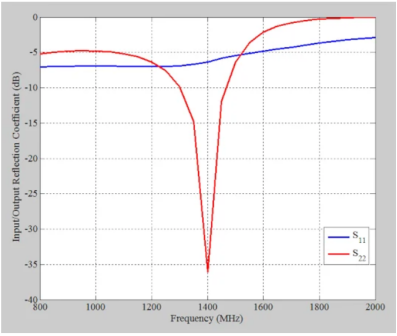
图7. 示例放大器在800 MHz至2000 MHz频率范围内的输入（蓝色）和输出（红色）反射系数。

示例3：为特定增益和噪声性能设计双边放大器

假设在f=1.4GHz时，我们研究的晶体管的噪声参数为：

Fmin = 1.6 dB

Γopt = 0.62 ∠ 100度

RN=20Ω。

使用这种晶体管，让我们设计一个噪声系数为3dB、最大增益与噪声系数兼容的放大器。

首先，我们找到NF = 3 dB恒定噪声圆的中心和半径。表3提供了所需计算的总结。请注意，我们在方程中插入了噪声系数，而不是噪声系数。

表3. NF=3dB恒定噪声圆总结计算。

图8绘制了NF=3dB的恒定噪声圆和例1中的恒定GA圆。

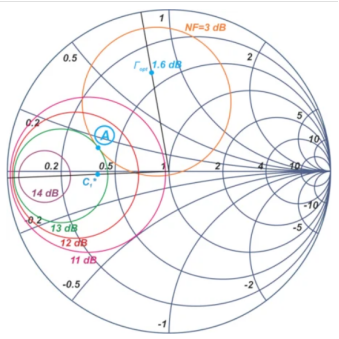
图8.示例1的恒定GA圆与3dB恒定NF圆并排绘制。

NF = 3 dB噪声圆与GA = 13 dB增益圆在点A相交，该点对应于ΓS = 0.46 ∠ 161.4度。确定ΓS后，我们现在可以找到晶体管输出端的反射系数：

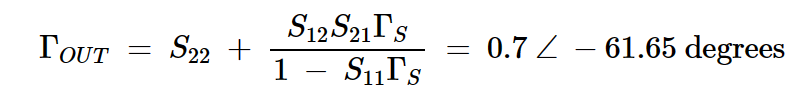
方程式17

最后，为了产生GT = GA = 13 dB，我们在输出端提供了一个复共轭匹配：

方程式18

我们将再次使用Z Smith图来设计匹配网络。图9和图10分别显示了输入和输出匹配网络的设计细节。

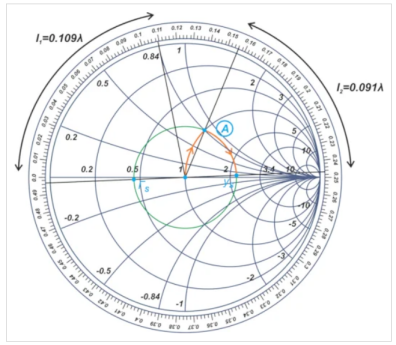
图9. 用于设计新示例放大器输入匹配网络的史密斯圆图。

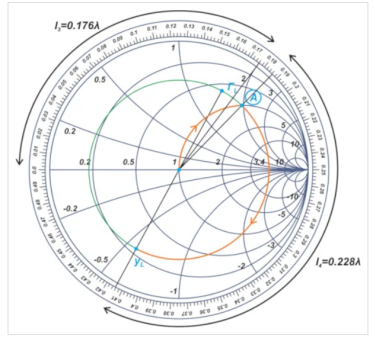
图10.放大器输出匹配网络设计的史密斯圆图。

图11显示了最终的交流原理图。

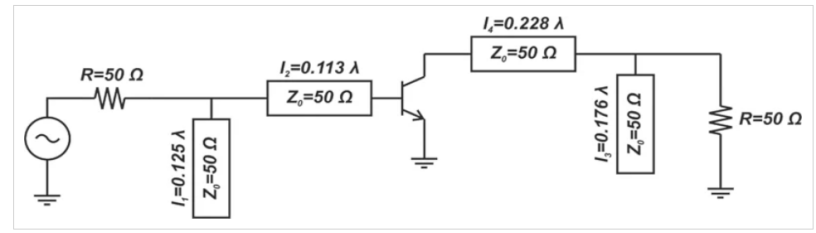
图11.双边LNA的交流原理图，该LNA的增益为13 dB，在f = 1.4 GHz时的噪声为3 dB。

对上述设计的计算机分析表明，在f=1.4 GHz时，增益为12.94 dB，噪声系数为3 dB。