假设这样一个场景：

有一个女孩Alice，她喜欢Bob，给他发了一封信‘我喜欢你’，另一个女孩Eve想搞破坏，拦截了这封信，篡改了它，再发给Bob，改为‘我不喜欢你’

我们可以采取什么措施实现：

• 交换机密/消息：除了目标接收方Bob，其他人都看不到消息的内容

• 保证消息的完整性：消息被Eve篡改后，Bob能识别出来

• （身份）认证：Bob要确定收到的消息确实来自Alice

这就需要密码学帮忙解决。

对消息进行加密

• 通过加密、解密机制，可以保证交换数据的机密性

• 两大类加解密机制：以AES为代表的对称加密算法和以RSA/ECC椭圆曲线为代表的非对称加密算法

• 加解密都需要密钥参与，只是对称加密过程中，加解密使用相同的密钥，而非对称加解密过程使用不同的密钥

对称加解密技术

• Alice和Bob事先约好了一个密钥

• 该密钥可以用来进行 加密消息，也可以用来解密消息

• 对称密钥系统的优势：简单快速

• 对称密钥系统的缺点：通信双方必须事先约好这个密钥，管理不方便

非对称加解密技术

• Alice和Bob事先自己产生自己的公钥-私钥对，私钥自己保存，公钥可以分享给其他人，不限于通信的双方

• 加密、解密使用不同的密钥，用公钥“处理/加密”消息，只能由与其对应的私钥来“恢复/解密”；用私钥“处理/签名”的消息，只能由与其对应的公钥来“恢复/验签”

• 非对称密钥系统的优势：密钥方便管理和分发

• 费对称密钥系统的缺点：实现复杂，运算效率不如对称密钥系统

二者的结合，各取优点

• 使用非对称密钥技术发送对称密钥；再使用对称密钥对大数据量的交互消息进行加解密，提供运算效率

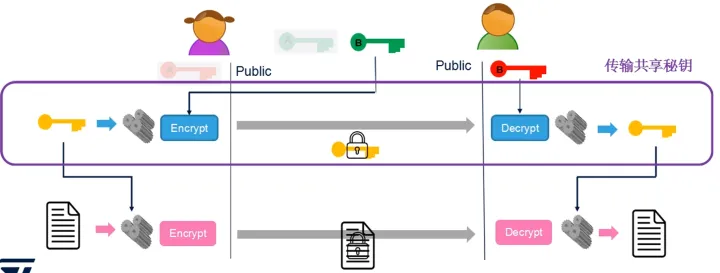
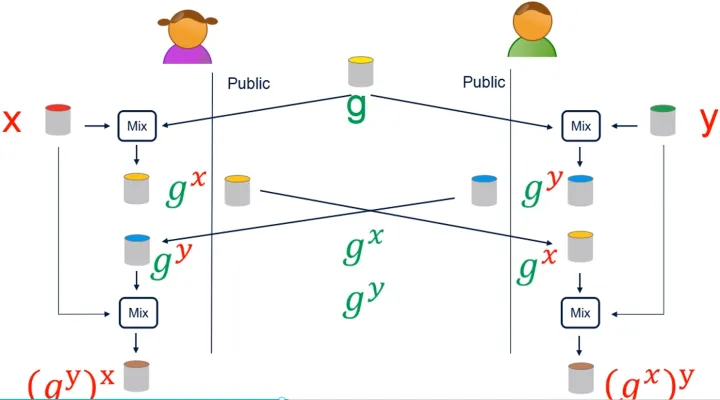
生成共享密钥

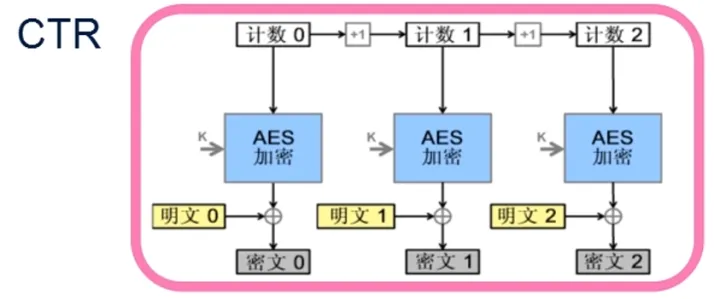
常用对称加密算法及模式

• 对称加密技术的特点：基于排列，组合，位移，异或等操作，因此软硬件实现起来都快

AES常用加解密模式

常用非对称加密算法

• 基于大数的数学运算，软硬件实现都较复杂，不适用于大量数据的实时加解密

RSA：密钥生成、格式

ECC：密钥的生成

DH算法/Diffie-Hellman，用于密钥协商

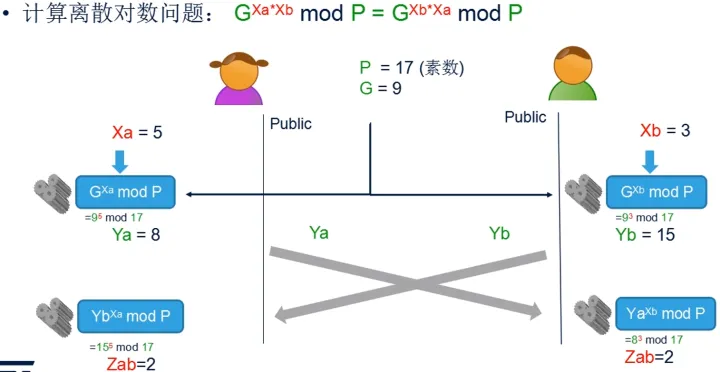
ECDH=ECC+DH