今天想聊下气密性测试时的泄漏率和压差的计算问题。通过搜索以及咨询别人，关于IP67对应的泄漏率标准的话，暂时无法通过计算和理论得来，可能有吧，但是目前不得而知。

于是通过之前的项目经验，即设定一个泄漏率标准，然后做些样品，将通过不同泄漏率标准测试的样品，再拿去做IP67测试。最后得出一个压差的变化速率经验值：就是测试样品的 压差变化速率在3~5pa/s(介质为压缩空气) 的时候，最终是能够通过IP67测试的。由于压差还与充气压力,腔体体积，时间等有关系，但是经验发现基本满足这个变化速率，可供参考。本文后面会基于这个数值做下泄漏率的换算。

目前大多数公司测试电控类产品主要通过压差测量法。其原理就是基于被测件和标准漏孔之间的压力差状态对比。然后测试设备系统具有压差和泄漏率的转换能力，并与设定的标准规格进行比较，从而判断是否合格。下图为一个压差测量设备的原理图：

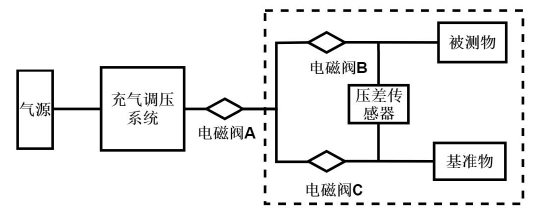
01

泄露率计算公式推导

通过经验我们假设了压差变化速率在3~5pa/s时，产品能够通过IP67的测试。接下来就需要知道如何通过压差来推导出产品的泄漏率。

在之前的文章中，我们已经知道了理想气体方程：

PV=nRT

现在我们假设在进行气密检测时的温度T保持不变；同时对产品充入一定量的气体，所以物质的量n也是固定的量；R为气体常数。

因此PV数值也是定量。

我们设定被检测产品的腔体体积为V1，充气结束时被充入的气体总量为n总，标准漏孔端的气压为Ps，被测产品端的气压为Pt，这个时候的Ps=Pt。

然后经过稳压和测试时间后，被检测产品有部分气体泄漏，设定泄露出去的气体的量为n2，体积为V2，标准大气压压强为P0,；此时被测产品残留的气体的量为n1，气压为Pu。设泄露率为Q。

那么：

n总=n1+n2;

(式 2-1）

于是PtV1=PsV1=n总RT

(式 2-2）

n总=PsV1/RT

(式 2-3）

同理：

PuV1=n1RT

(式 2-4）

n1=PuV1/RT

(式 2-5）

n2=P0V2/RT

(式 2-6）

根据式2-1可得：

PsV1=PuV1+P0V2

(式 2-7）

那么V2=（Ps-Pu）V1/P0

(式 2-8）

因此泄漏率为：

Q=V2/t=(Ps-Pu)V1/P0t

(式 2-9）

Q的单位为ml/min,P0=1.013e^5pa。

令△P=(Ps-Pu), 压差变化速率为δP=△P/t，因此式2-9可变化为：

Q=δPV1/（1.01310^5）=0.9910^-5δP*V1(ml/s)

(式 2-10）

将Q的式2-10的单位再换算成ml/min,于是得：

Q=0.9910^-5δPV160≈610^ -4 δP*V1(ml/min)

(式 2-11）

我们也可写成常用的形式：

• Q=V （△P/P0）（60/T） *

其中Q为泄漏率，单位为ml/min;

V为被测产品腔体体积，单位为ml;

△P为压降，单位为Pa;

T为测试时间，单位为s。

P0为一个标准大气压，等于1.013e^5pa。

02

案例计算

现在已知一个电控产品需要满足IP67，而且其内部腔体体积V为286ml；产品的整机测试压力为57.2Kpa；检测时间为20s；试定义产品的初始泄漏率标准。

解答：

根据经验产品满足IP67时的压降变化速率为3~5pa/s,因此根据式2-11可知：

Q≈610^ -4 δPV= 610^ -4* 3*286≈0.51ml/min;

Q≈610^ -4 δPV= 610^ -4* 5*286≈0.85ml/min;

因此初始的泄露率标准可定义在0.51~0.85ml/min。

03

其他相关信息分享

1.单位换算关系：

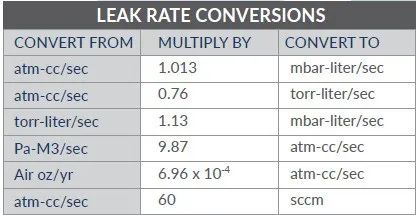
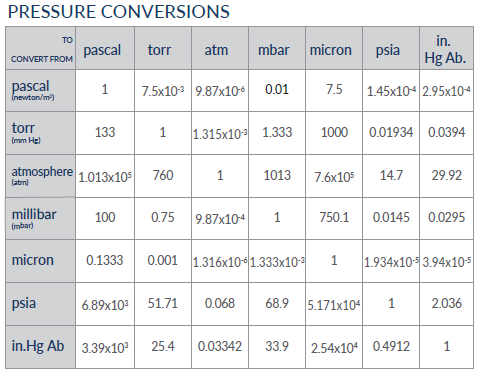
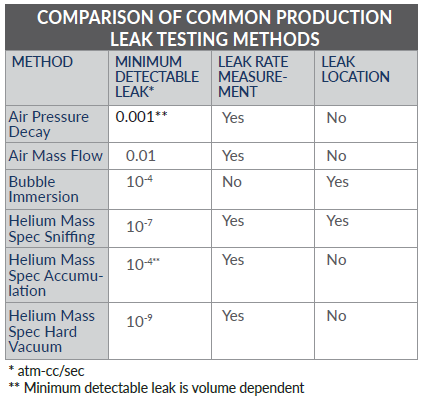
2.不同泄露测试方法比较：

3.等效泄漏率 ：****

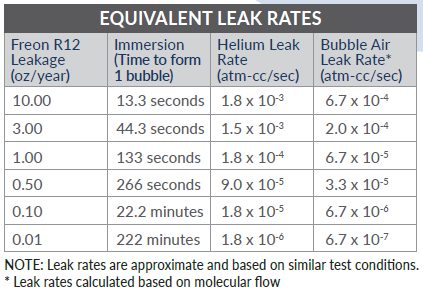
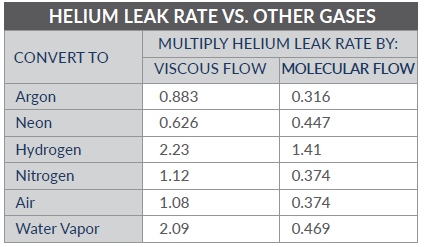
4.氦检泄 漏率与其他气体泄漏率的换算关系 ： ****

写在最后

在某些充气压力较小的情况下，比如3Kpa，此时就不适用3~5Pa/s的压降变化率经验值。因为本身气体压力就小，所以压降变化率自然也需要变小。

据我的经验，这个值我所遇到的适用充气压力范围为20~270Kpa。

如果超过或者小于上述的范围，需要重新经过实验，找到合适的经验值。