在功率超声领域，作为一种重要的“电-声( 力)”转换元件，其性能的优劣直接关系到整个功率超声系统的工况性能及效率。大量的应用场景需要具备稳定的输出特性以及较高的能量转换效率，能够在长期连续的大功率条件下可以稳定输出超声波能量。针对性能的评价方法，1995 年，颜忠余、林仲茂^[1]从理论上分析了换能器的结构和材料参数对其性能指标的影响，以及不同外部负载条件下这些参数对换能器性能的影响，并提出正确设计的方法。2001 年，俞宏沛等^[2]通过建立在小功率激励与额定大功率有载激励．只要使其振动幅度相等则换能器振动的动态疲劳及损伤程度是近似相等的原则之上，对换能器在的条件下激励，使其振动幅度等于有载下的标准参数值，使换能器在较小的功率级下进行较大的振幅下长期激励振动后通过评价有效机电耦合系数keff 和机械品质因数Qm 与初始值的变化量来衡量换能器损伤与否。2007 年，Riera E 等^[3]通过搭建基于LabView 的大功率换能器测试平台，监测大功率激励条件下换能器端的功率、阻抗、相位、振幅、温度等多参数的数据，对测试样品换能器进行综合数据分析和评价。

从上述内容不难看出，目前针对换能器性能的评价，国内研究者主要基于小信号等效参数的评价，尚缺乏大功率激励时换能器综合表观参数与小信号等效参数的相关性研究，而国外研究者开展了换能器的多种参数的综合评价，但其测试设备昂贵和精密，导致应用场景非常受限。本文基于上述研究，通过将换能器与实际大功率激励条件下换能器温度变化表观参数的相关性进行分析，研究小信号测量条件下的与实际大功率激励条件下的换能器表观参数的相关性，建立了一种简便、高效的利用综合效率评价换能器性能优劣的方法。

1 理论分析

1.1 换能器的力学等效系统

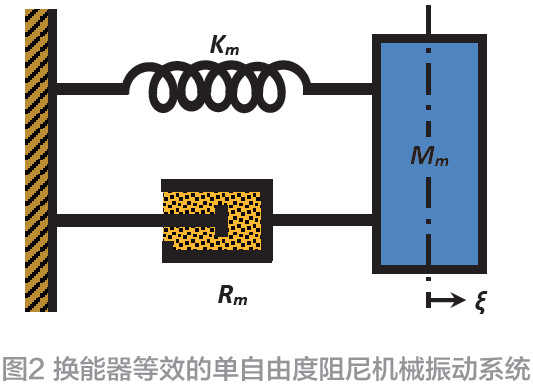
在功率超声应用中，压电换能器常采用“夹心式”结构（Sandwich constructions），图1 为其典型结构示意，该结构一般由前辐射块、压电陶瓷以及后部背衬通过一定数值的预应力（预应力一般约为30 MPa）构成了一种力学串联形式。图2 为该结构换能器的力学等效模型。在不考虑负载的条件下，可以将其等效为如图2所示的一个质量为Mm 的作单自由度运动的物体连接在弹性系数（刚度系数）为Km 的弹簧上所构成的“单自由度阻尼机械振动系统”，其中Rm 为弹簧做功时的阻尼，ξ 为质点的位移量。当质点Mm 被外力沿固定轴方向推离平衡点时，弹簧也同时产生拉伸形变，假设此时质点位移量ξ 未超出弹簧的弹性限度，根据胡克定律，其弹簧的弹力F_k与质点位移量ξ存在以下关系^[4]

通过式（1）可见，弹簧弹力F_k与质点位移量ξ成正比，并根据牛顿第二定律，可以将式（1）改写为

其中a为质点M_m加速度，而加速度a即为位移量ξ的二阶导数，因此可以将式（2）改写为

以上是在未考虑阻尼R_m的情况，而将R_m引入后则可将式（3）改写为

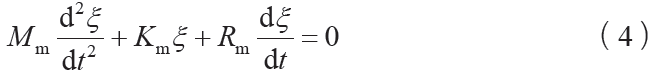
1.2 换能器的电学等效系统

考虑到求解电学问题的方法相较于力学更丰富和完善，在处理一些机械振动问题时可以利用相应变量物理意义的类比进行电学网络等效^[5]。因此，类比于力学系统的各变量的物理意义，可以将力学系统中的作为惯量形式存在的质量M_m等效为电感量L_e，将储能形式存在的弹簧弹力K_m等效为电容量C_e，将机械阻尼R_m等效为电阻R_e，并形成如图3 所示的一个串联形式的RLC等效电路。

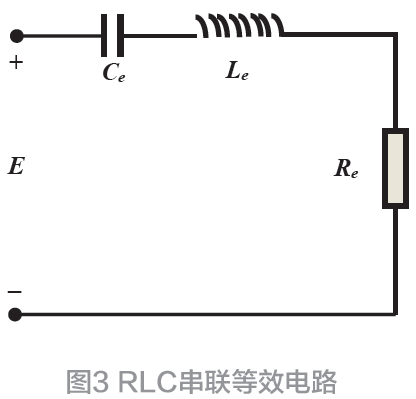
该电路中具有一个电场为E 的恒压源，而各等效元件以串联的形式连接构成了一个闭合回路，类比于力学系统，电场E即为力学系统中F在电学上的表现形式，而电流I则为力学系统中v在电学上的表现形式，则在闭合回路中的各等效元件具有以下的表现关系^[4]

瞬态条件下等效电感

瞬态条件下等效电容

等效电阻

根据基尔霍夫第二定律可知，闭合回路中各元件上的电压的代数和恒等于0，则可将上述等效电路表示为

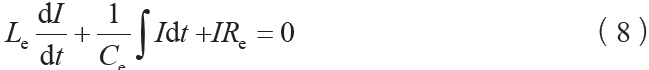
以上是针对力学系统与电学系统的类比推导，可见两个系统之间可以通过各元件在各自系统中所起的作用进行等效对应，这对于理解换能器的工作机制具有十分重要的意义，但对于功率超声换能器而言，其电声转换效率的高低直接关系到换能器性能的优劣，特别是动态参量N_eff可以较为全面的反映换能器结构、材料、工艺等多方面的性能指标^[1]。其表达式为

其中，Q_e为电学品质因素，Q_m为机械品质因素，K_eff为有效机电耦合系数，这些参量的表达式分别为^[6]

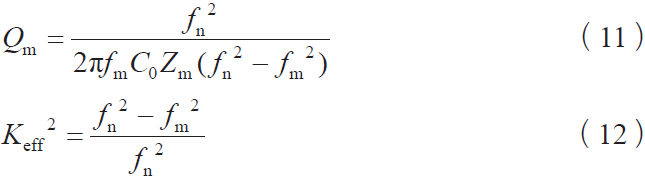
通过式（10）可以理解为Q_e与介质损耗成倒数关系，并且其还有另一种表达式^[7]，即

其中，ω 为测试换能器静态参量时的角频率，C₀为静态电容，R为静态条件时的损耗电阻，而式（11）、式（12）中的f_n、f_m、Z_m分别表示为反谐振频率和谐振频率，以及最小阻抗值。而式（12）也可以通过换能器的电容比进行表达^[7]，即

综合以上对换能器各的推导后可以获得一个包含C₀、tanδ、Z_m、L₁、C₁这五个因素所构成的换能器等效模型，其中，C₁为谐振状态下的动态电容。并可以通过该模型得到与之对应的Neff 变化规律，经过归一化后上述五个因素与Neff 的对应关系如图4 所示。

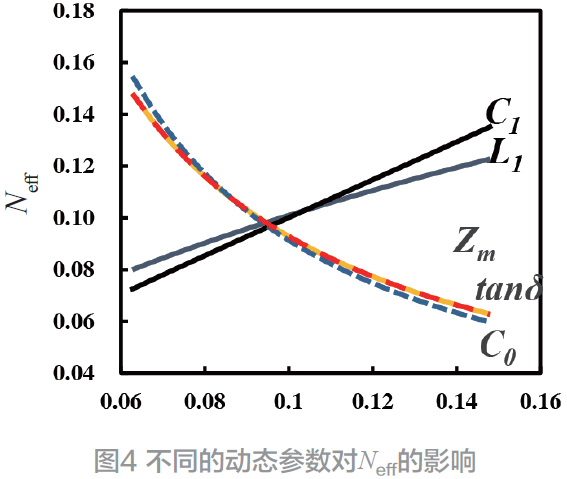
正如之前所推导的情况，通过图4 可见，动态参数C₁、L₁对N_eff起到了正面影响，而Z_m、tanδ 及C₀对N_eff起到了负面影响，并且这三个因素影响程度相较于C₁和L₁更为显著。

2   实验过程

实验目的主要为验证换能器的小信号与实际大功率激励条件的表观的对应关系。实验中分别选取了四种不同特性的PZT-8 压电陶瓷材料，同时利用相同的换能器金属结构部件和安装工艺参数装配形成如图5、图6 所示的具备了换能器、变幅杆以及工具头的完整样品，并先通过阻抗分析仪采集各样品的参数后，按式（9）计算得出相应样品的N_eff数值。如图7 所示，再利用大功率激励信号源在无载条件（空气中）下进行时长30 分钟的大功率激励，同时利用红外热成像仪记录换能器各标志点温度变化数据后求解出换能器积温率（Rate of accumulated temperature）进行比较。其积温率表达式为

其中，ΔT 表示换能器各标志点温差，t表示为积温时间。

图5 实验中所制作的换能器样品

图6 实验中制作的完整样品

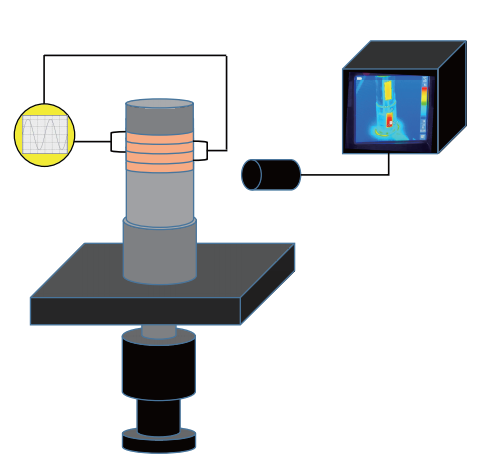
图7 实验中的测试系统示意图

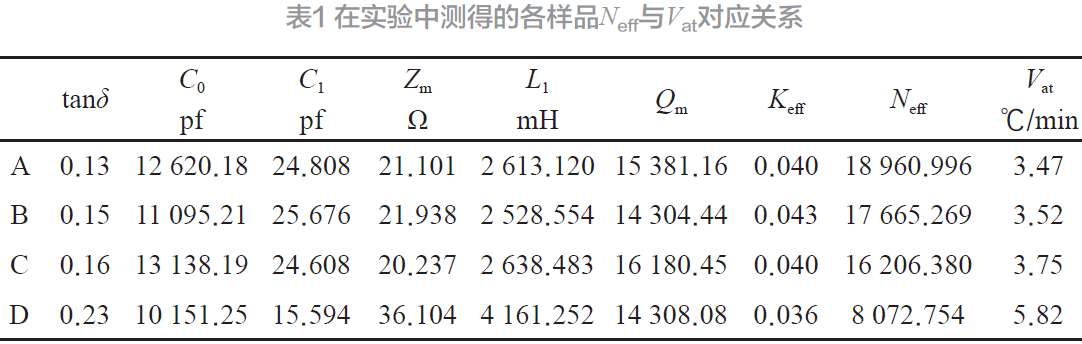
表1 显示了利用上述方法获得的各实验样品的相关电学等效参数和动态参量N_eff以及与之对应的换能器积温率V_at。通过表1 所示数据可见，N_eff与V_at具有相关性联系。

3   结果

通过上述实验可以验证换能器的综合参量N_eff与换能器在大功率激励条件下的温升呈现负相关性，随着N_eff的增高，换能器的整体的温升速度也随之降低。并且，就换能器的集总参数而言，明显可见介质损耗tanδ与N_eff之间呈现了明显的直接相关性，而C₀、C₁、L₁由于具备一定的关联属性，直接相关性不明显。

利用上述实验结果，将N_eff作为自变量，而将V_at作为因变量进行线性回归分析^[8]，并从表2可以看出，模型公式为：V_at= 0.457-0.829×N_eff，模型R方值为0.989，意味着N_eff可以解释V_at的98.9% 变化原因。对模型进行F 检验时发现模型通过F 检验(F = 174.975，p = 0.006<0.05)， 也即说明N_eff一定会对V_at产生影响关系， 最终具体分析可知：N_eff的回归系数值为-0.829(t = -13.228，p = 0.006<0.01)，意味着N_eff会对V_at产生显著的负向影响关系。

4   讨论

通过图8 可以看到，对于一个完整的换能器而言，N_eff与V_at呈现负相关性变化，即N_eff数值越大，其所对应的V_at也越小。同时，利用数据的线性回归分析结果也可知，N_eff全部均会对V_at产生显著的负向影响关系。当C₁与C₀的比值达到0.002时，并且C₁与L₁的比值达到0.01 时，换能器的整体N_eff值将处于一个相对较高的水平，其温升率则较低，换能器性能优异。而当换能器的上述比值分别低于0.0018 以及0.009时，换能器的N_eff值偏低，温升率则会偏高，换能器性能劣化趋势显著。综上所述，通过对于换能器的集总参数等效模型与实验的结果可见，换能器动态参量N_eff可以较为全面地反映换能器的性能水平。并且可以发现，实际的大功率激励后换能器的表观积温率V_at与动态参量N_eff之间存在相关性联系，通过直接获取换能器V_at数据并结合N_eff的比较可以简便和迅速的评价换能器的性能水平的优劣。而通过等效模型分析并结合实验结果可知，提高换能器的动态电感L₁、动态电容C₁并保持与静态电容C₀的一定比值，同时降低阻抗Z_m和介质损耗tanδ，则可以获得较高的动态参量N_eff值。因此，基于本文的研究结果，特别是针对不同条件或状态下，换能器的动态参数与静态电容之间的比值与N_eff 的对应性也将是后续研究的一个重要方向。

参考文献：

[1] 颜忠余,林仲茂.夹心压电换能器的优化设计─分析各参数对换能器性能的影响[J].声学学报,1995(1):18-25.

[2] 俞宏沛,费国强,方玲.用寿命试验来评估声呐换能器[C].全国船舶仪器仪表二00一年学术会议.中国仪器仪表学会;中国造船工程学会,2001.

[3] Riera E , Juan A Gallego-Juárez, Blanco A , et al. Power characterization of ultrasonic piezoelectric transducers[C]. International Congress on Ultrasonics, ICU 2007. 2007.

[4] 杜功焕,朱哲民,龚秀芬.声学基础.2版[M].南京:南京大学出版社,2001.

[5] 滕舵,杨虎,李道江.水声换能器基础[M].西安:西北工业大学出版社,2016.

[6] 佚名.Piezoelectric Ceramics: Principles and Applications[J]. 2011.

[7] 林书玉.超声换能器的原理及设计[M].北京:科学出版社,2004.

（本文来源于《电子产品世界》杂志2022年4月期）