引入
卡尔曼滤波是通过对下一时刻系统的状态估计以及测量得出的反馈相结合,最终得到该时刻较为准确的的状态估计(预测+测量反馈),我们一般所说的卡尔曼滤波KF是针对线性系统的,其思想对于非线性系统也是适应的,由此延伸出来的有EKF,UKF等。
我们先从简单的问题入手,来了解卡尔曼滤波的思想
假如我们想知道一枚硬币的厚度,并且有k个测量值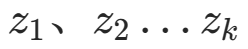 ,为了估计真实值,我们一般对其取均值,于是估计量
,为了估计真实值,我们一般对其取均值,于是估计量
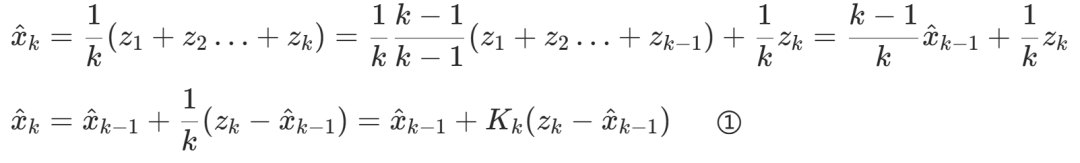
由①式知,当我们只有一个测量值时,即k = 1,我们只能选择相信测量值,而当k —>∞时,我们可以相信上次的估计值。且本次的估计值只跟本次的测量值和上次的估计值有关,不用再追溯到前k-1个测量值
其中Kk为卡尔曼增益,为使估计误差最小,我们使方差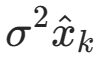 最小,令
最小,令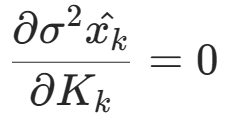 得
得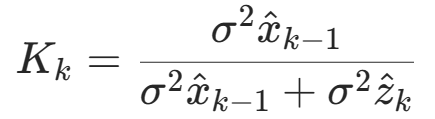 ,并做下式变换得卡尔曼增益的一般形式,此Kk值具有数学上的最优性
,并做下式变换得卡尔曼增益的一般形式,此Kk值具有数学上的最优性
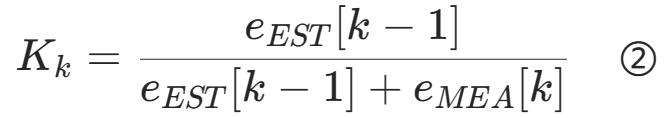
eEST为估计误差,eMEA为测量误差。观察②式知,当e EST ≫eMEA时,Kk = 1,将带入①式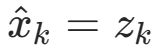 ,即当估计误差比较大时我们选择相信测量值。相反,当e EST ≪eMEA时,Kk = 0,
,即当估计误差比较大时我们选择相信测量值。相反,当e EST ≪eMEA时,Kk = 0,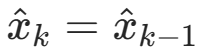 ,此时我们选择相信估计值
,此时我们选择相信估计值
该情形下卡尔曼滤波的一般步骤:
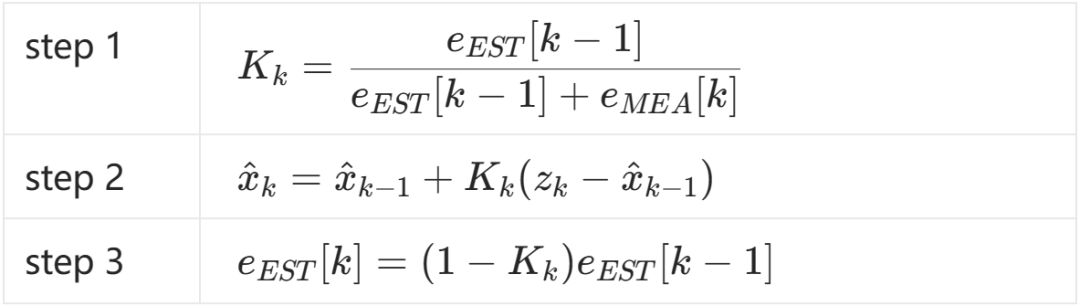
卡尔曼滤波器
考虑系统
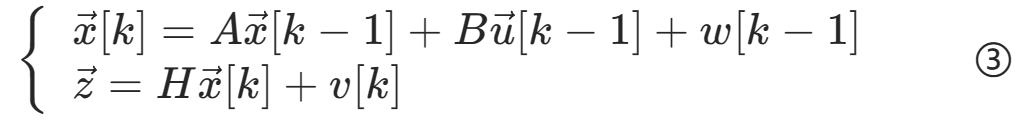
其中ω为过程噪声,服从N(0,Q)分布。υ为测量噪声,服从N(0,R)分布
1、协方差矩阵
将方差和协方差通过一个矩阵进行表示
方差:

协方差:
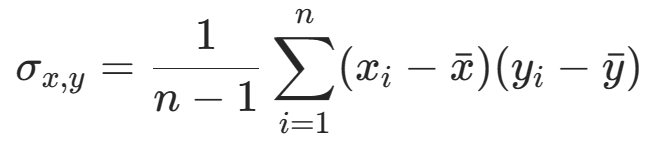
考虑以下三阶的协方差矩阵
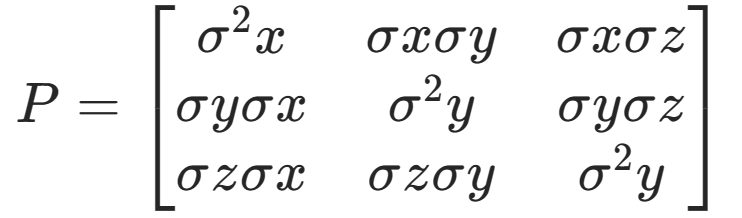
构造过度矩阵T求此协方差矩阵,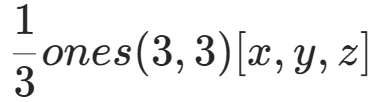 构成了
构成了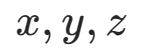 的平均值矩阵
的平均值矩阵
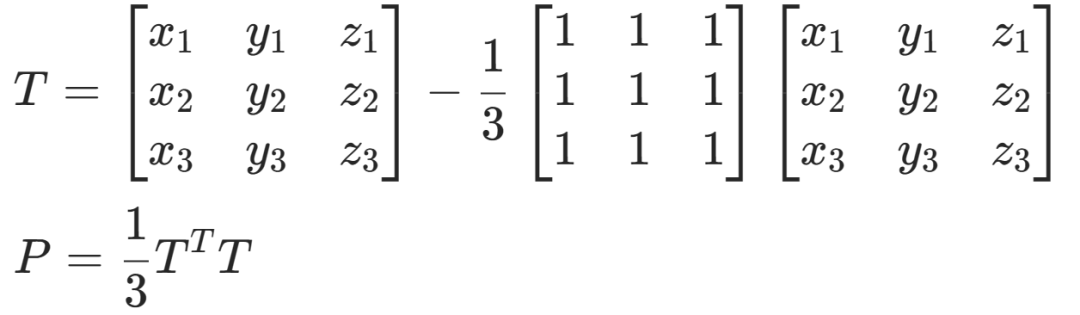
对于③式表示的系统
由于D(X) = E(X ^2^ ) - E ^2^ (X),而E(ω_i) = 0,于是协方差矩阵可由下式表示
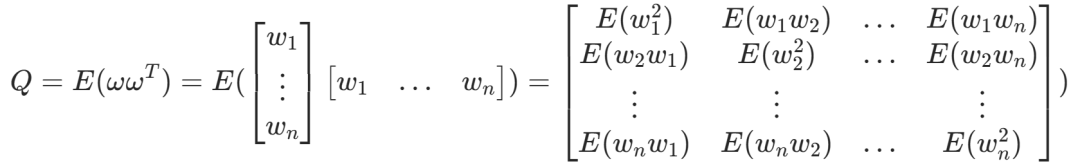
同时,ω 1 、ω 2 、… 、ωn相互独立
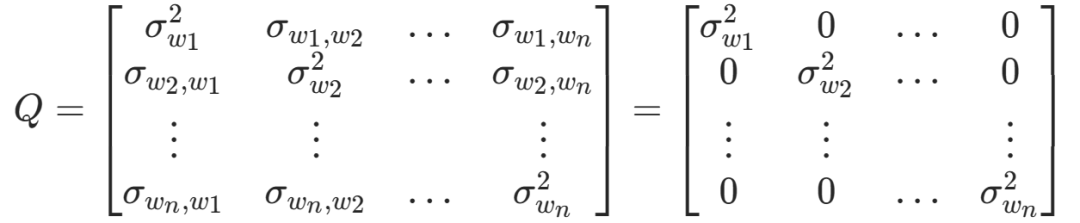
同理R = E(υυ ^T^ )
2、先验估计
没有考虑过程误差和测量误差,由状态空间方程计算所得
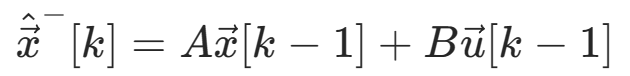
但是在电机模型中ω和θ无法获得,我们可以将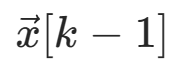 替换为
替换为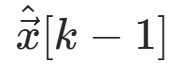 同时由测量
同时由测量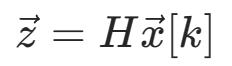 得,
得,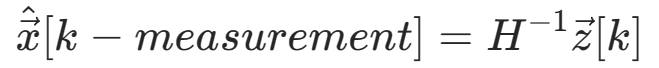
3、后验估计
估计+测量反馈
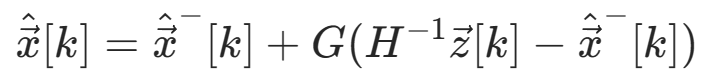
令G = KkH,则
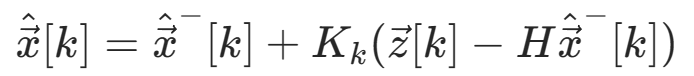
4、卡尔曼增益
卡尔曼增益Kk是凹函数的极点,因此卡尔曼滤波器既是一个观测器,又是最优性估计
令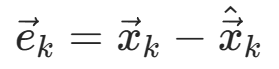 ,服从N(0,P)分布
,服从N(0,P)分布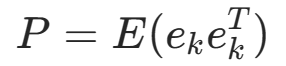
为了使tr(P)最小,即方差最小,令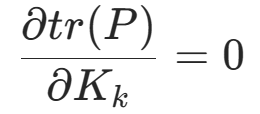 得
得
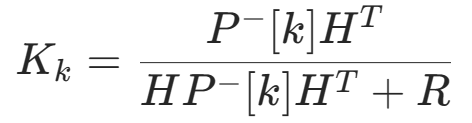
具体推导过程可参考B站UP主DR_CAN,视频链接放在文末
其中P ^-^ 为先验误差
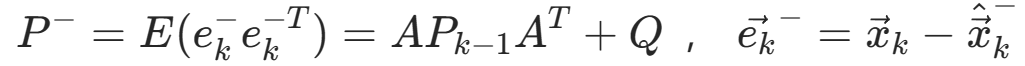
卡尔曼滤波的一般步骤

电机状态方程
上文龙伯格观测器中我们选取了状态向量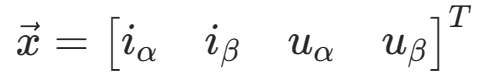 ,但是为了利用卡尔曼滤波器对ω和θ进行预测我们选取状态向量
,但是为了利用卡尔曼滤波器对ω和θ进行预测我们选取状态向量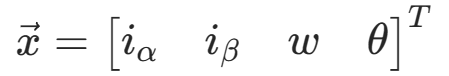 ,测量向量
,测量向量 ,并将反电动势形式做如下修改(电流滞后电压90°,因此α轴的反电动势由β轴电压产生,并且反向)
,并将反电动势形式做如下修改(电流滞后电压90°,因此α轴的反电动势由β轴电压产生,并且反向)
1、状态向量
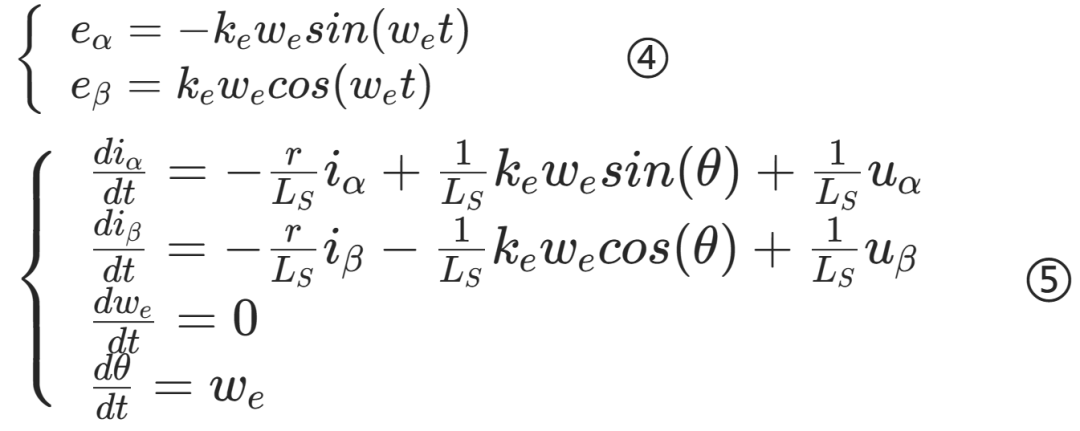
2、线性化
此时该系统是一个非线性系统,为了利用卡尔曼滤波我们要先对其进行线性化,用EKF对系统状态进行估计,令
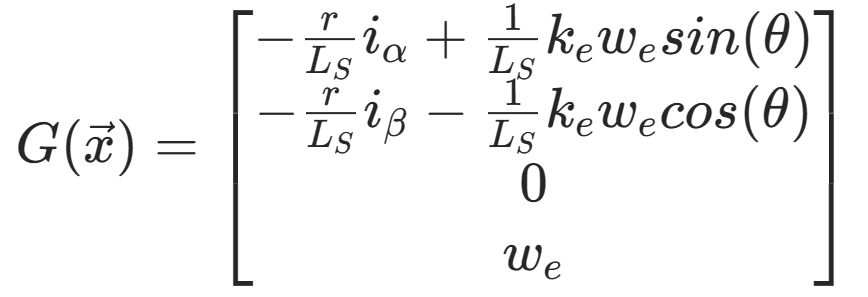
在先算先验估计时用的是未经离散化的非线性函数
对上面卡尔曼计算一般步骤①先验估计做如下更正,其他步骤不变
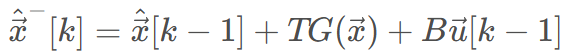
雅可比矩阵
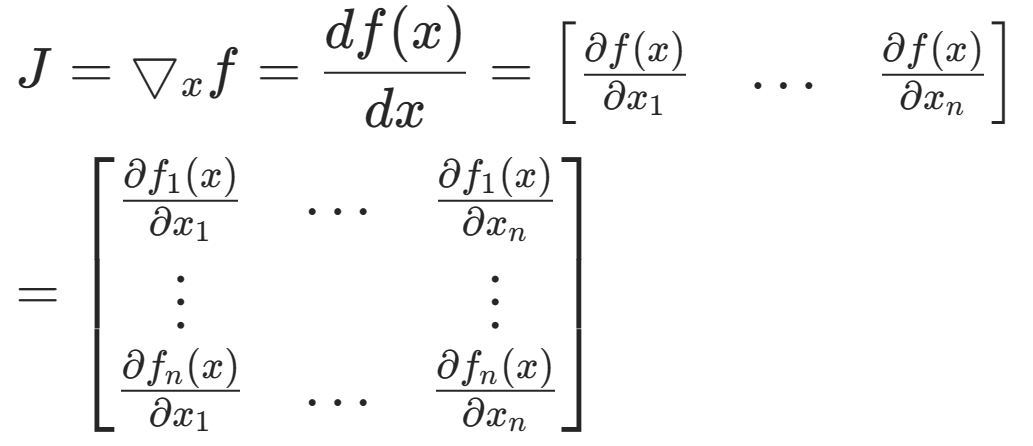
于是
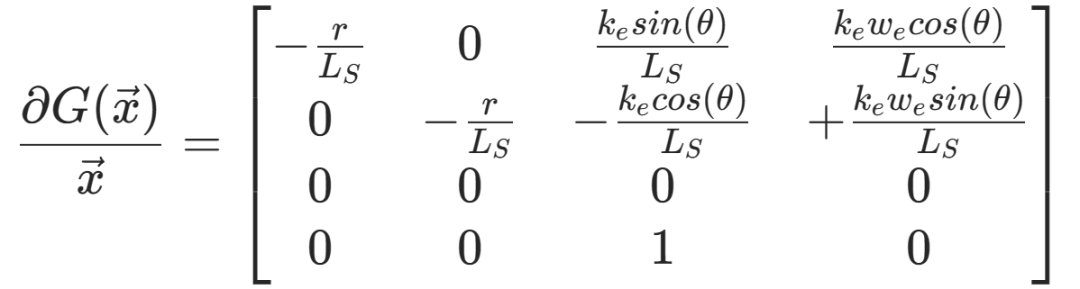
3、离散化
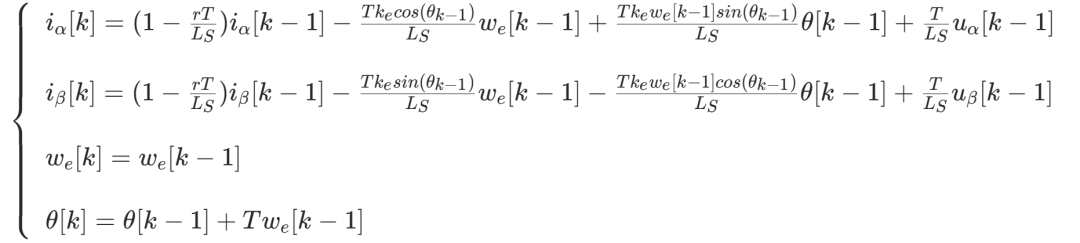
于是线性化后的离散系统矩阵

MATALB仿真
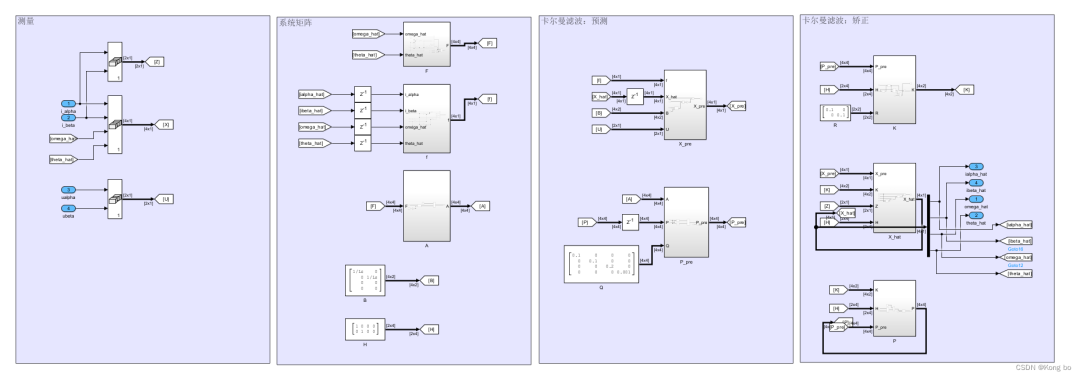
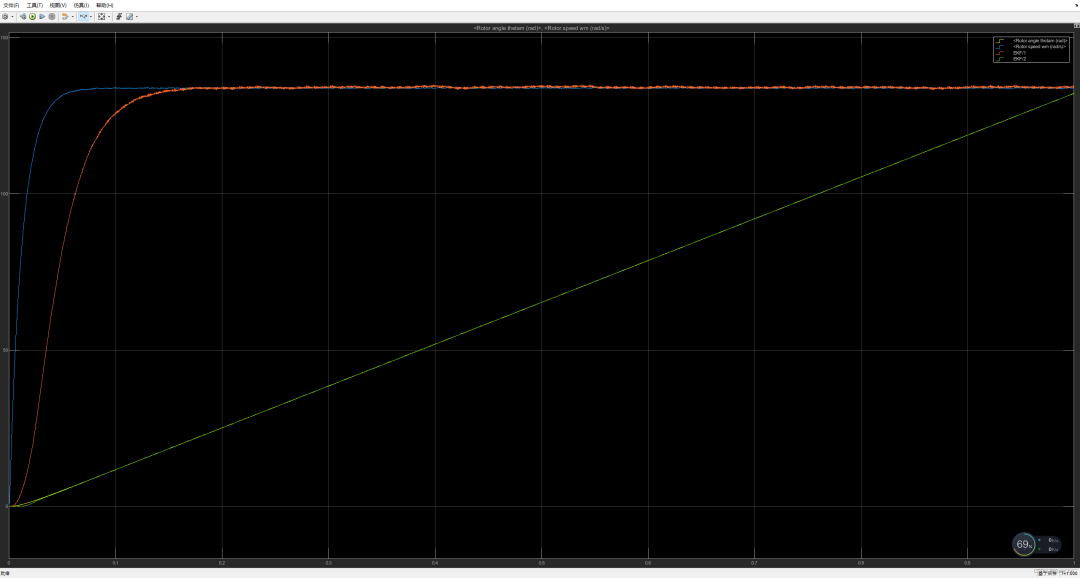
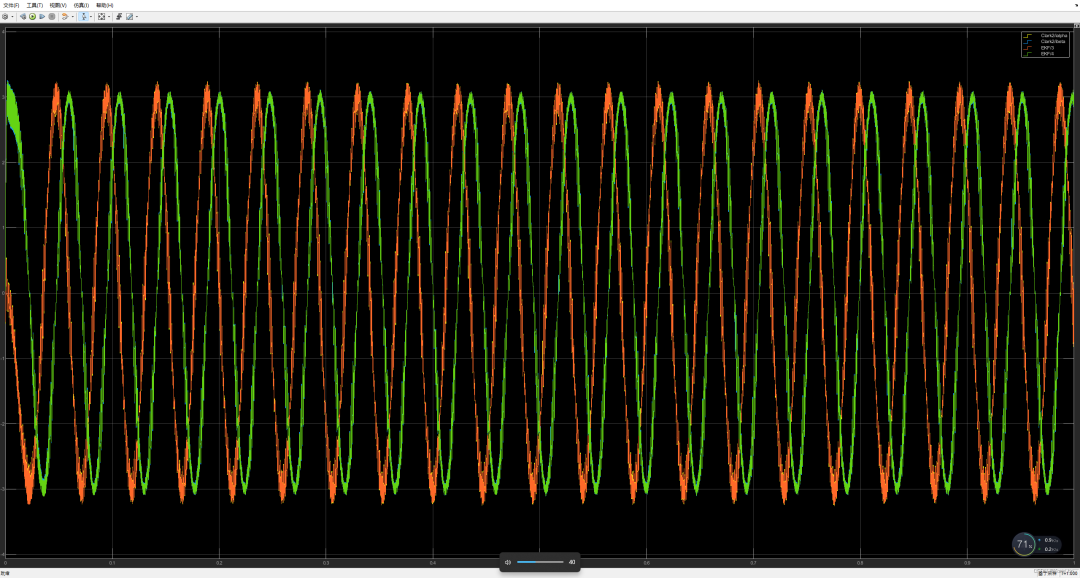
EKF
可以看到卡尔曼滤波器的θ估计输出几乎与实际位置重合,速度估计ω受磁链常数影响,磁链给的偏大会导致ω估计偏小,相反磁链给的偏小会导致ω估计偏大,推荐对θ微分作为ω的估计