遥想当年，与傅里叶变换（Fourier Transform）的第一次偶遇是学习信号与系统的时候，觉得她的数学表达很美，想进一步了解来着，但终究只可远观而不能领会其奥义，对她的理解仅仅限于一种数学变换，考试的时候会算算矩形窗的傅里叶变换，按部就班的演算，仅此而已，驾驭不了她，从此形同陌路。

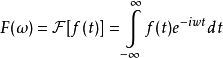
图1 傅里叶变换，简洁优雅，貌美如花

转机出现在学习OFDM(正交频分复用)的时候，调制与解调是通信的核心部分之一，OFDM的调制与解调却能用傅里叶变换对如此简洁而深刻的表述，感叹不已。傅里叶第一次在我心中有了如此清晰的，初步的物理概念。我一直觉得数学家很厉害，因为任何抛开实际物理概念的数学演绎都是极其抽象的，要想清楚并不容易，数学的抽象与严谨而没有附加物理概念的直观是我们惧怕数学的重要原因不是吗。冰冷的数学公式被赋予清晰的物理概念而变得如此鲜活，就如广义相对论之于黎曼几何，杨 · 米尔斯规范场之于纤维丛理论。所以呢，了解傅里叶变换的钥匙就是物理概念。

所谓条条大路通罗马，不同领域，不同物理或工程角度都给解读傅里叶变换提供更多可能性，而雷达特别是车载雷达角度的解读是很有意思的，所以此文尝试以毫米波雷达视角全面阐述傅里叶变换的物理概念及外延，希望对你有收获。能够加深你对她的深刻理解。

在车载雷达应用中，我想很多小伙伴知道对ADC Raw Data做1D FFT，对一维数据做2D FFT，DoA则是3D FFT，如同我们会算rect(t/T)的FT是sinc(w)一样，但我们可能对其背后的物理概念及外延并不清楚，比如如何理解三个维度都可以做FFT，为什么要做FFT，FFT达不到要求怎么办，不做FFT行不行等等。如图2所示公式是单目标MIMO雷达回波表达式，也是当前车载雷达使用最普遍的回波模型之一[1]：

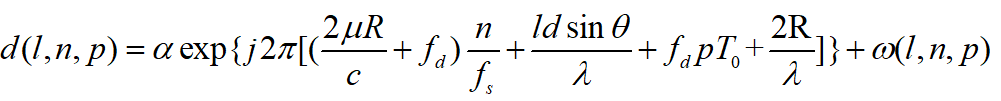
图2 automotive MIMO Radar 回波表达式（单目标）

它有3个维度，l，n，p，分别代表角度bin，距离bin，速度bin，所以在各自维度的取值范围内，d(l,n,p)表示一个数据立方体，也叫做radar cube, 如图3，我们对该cube分别沿range axis, Doppler axis, Space axis做FFT，以提取range, Doppler,以及 Azimuth信息。这是作为雷达算法工程师认识FT的第一层次---知道操作流程，也就是怎么做的问题。

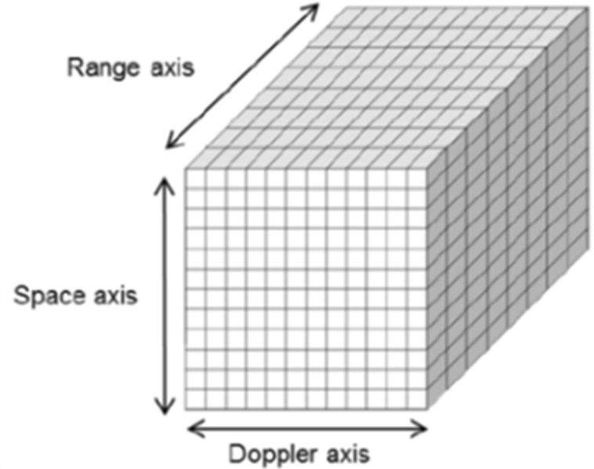
图3 Radar Cube

接下来我们依次对三个维度中的两个维度取定值，继续将d(l,n,p)拆解为3个维度：

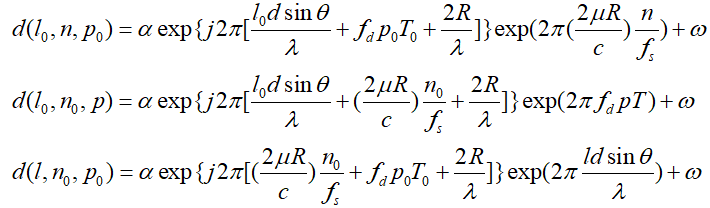
其中高斯白噪声表达做了简化，上述3式可以进一步归纳：

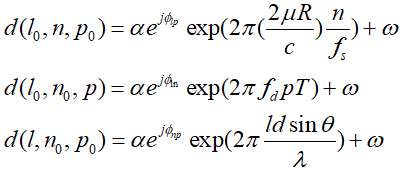
我们发现每个公式开头其实都是常相位，所以还可以简化并整理：

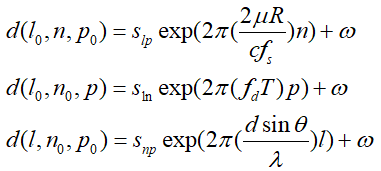
可以看到上述3式的质都是相同的，都具有如下形式：

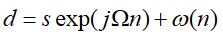
这也是为什么3个维度都可以做FFT的原因。另一方面，我们关心的距离速度方位角信息都包含在一个相对应的频率之中，信息与频率是一一对应的，所以信息的获取转化为频率的提取，而FFT就是提取频率的重要工具。

那么问题又来了，为什么提取频率的不是其他工具，而是偏偏FFT呢？

继续分析，实际工程中，我们得到的是d,而d是包含噪声的，也就是上式中的w。通常，我们假设该噪声是高斯白噪声，那么问题又转化为，高斯白噪声条件下的频率估计问题，再来捋一捋，

1 我们有什么，有量测，也就是含噪数据

2 我们假设什么，包含噪声是高斯白噪声,也就是知道分布

3 我们要干什么，估计频率

基于上述1，2，3，我们应该想到似然函数, 上述问题的似然函数为：

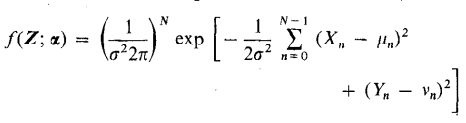
具体推导可以参考文献[2]，这边不再赘述，从推导结果来看，高斯白噪声条件下频率估计的最大似然结果就是FFT:

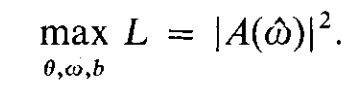
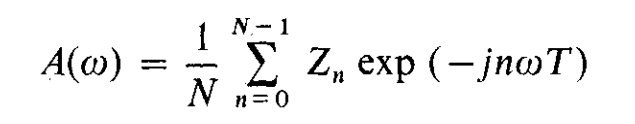
其中L是似然函数，A(w)是FFT，这是认识FT的第二层次--追根溯源，知道为什么要用FFT。应为她在似然准则下估计频率是最优的。

如前所述，FFT归根结底还是频率估计的工具，能不能用其他方法代替呢？回答这个问题取决于你的应用，雷达输出三个量：距离，速度，角度，而评估这三个量的重要指标是分辨率及精度，根据应用的不同，我们对分辨率及精度的要求是不同的，当然，如果条件允许，当然希望分辨率及精度越高越好。傅里叶变换已经很优秀了，而且还有快速算法的加持，使她在车载雷达等嵌入式平台独领风骚，叱咤风云数十载。但我们始终要用发展的，变化的，审视的眼光看问题。是的，那么优秀的FFT也是有瑕疵的：

• 存在瑞利限，分辨率（resolution）不高

• 旁瓣（sidelobe）容易引起虚警(High False Alarms)

• 频率是时间统计的平均频率，缺乏时间局部频率信息

• 多目标条件下，频率估计精度较差

FFT的瑕疵使得雷达估计那三个量的分辨率及精度较差，也就可能满足不了你的应用需求。基于此，数十年来，在争夺频率估计权力的征途上，各路豪杰层出不穷，好精彩！

傅里叶是分析信号处理的鼻祖，而各个时代的大佬基于前人的工作及自己独到的见解逐步发展出贝叶斯估计框架，状态滤波，认知信号处理，以及机器学习或者神经网络的方法，我们希望在硬件算力及内存允许的条件下，逐步将这些方法用于那3三个量的更好的估计，特别是角度这一块，这是认识傅里叶的第三个层次--继往开来，这不是对FFT的否定与抛弃，而是继承与发展，这些方法也被统称为现代数字信号处理方法，将会在今后的文章中介绍和分享！

FFT依旧是无穷无尽的宝藏，时常回头看看她，依旧如沐春风，心生敬畏，如同漂泊异乡的我们再成功，每每踏上故土，是不是也会感慨万千：

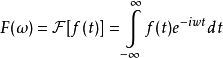
图4 让我再看你一眼，别来无恙