针对汽车 IGBT 模块的主要失效原理和引线键合寿命短板，结合仿真分析进行了功率循环试验设计，结温差ΔTj 和流经键合线的电流 IC 是影响键合点寿命的主要加速因子，中间温度（Tjm）是影响键合点寿命的重要因子。传统功率循环寿命试验需采用大量的试验样本，文章采用单根键合引线作为试验独立样本，极大程度地减少了试验所需的样本数，同时通过压降参数 VCE(sat)的微小变化相对准确地获取到 IGBT 模块内部键合线的脱落趋势，结合寿命模型和威布尔统计方法，对键合点寿命进行统计分析，最终获得功率循环寿命曲线。利用新的功率循环寿命统计方法可将试验成本和试验周期减少 80%。

0 引言

随着电动汽车的高速发展，作为其核心部件的IGBT 模块的可靠性也倍受关注。IGBT 的寿命研究国内外已有不少研究成果，但是对于汽车用的 IGBT 模块的研究较少。汽车 IGBT 模块应用工况相对其他应用工况更加恶劣，在汽车运行过程中，启停和加减速频繁，对应的是 IGBT 模块的功率变化，IGBT 结温也会随之不断循环变化，温度变化产生的热应力会使模块内部层次间产生蠕变热疲劳，直至 IGBT 失效。针对汽车IGBT 特殊的应用工况条件，准确地评价 IGBT 模块的热循环寿命需求非常迫切。

功率循环试验是 IGBT 模块常用的加速寿命试验方法之一，通过给 IGBT 模块通断直流电流并结合外部冷却水冷却，使芯片结温在可控的温度范围内变化，该方法是通过加速方法模拟 IGBT 模块在应用工况中的温度变化，定量评价热疲劳的损伤，是应用寿命预测重要的评价手段。

1 功率循环寿命退化原理

服役状态下的 IGBT 模块处于亚稳定状态，其材料和结构会随着时间的推移发生状态改变或退化。IGBT 模块在整个寿命周期内，会经历数万至数百万次的温度循环冲击，这期间热应力的反复作用会使材料发生疲劳，造成模块封装结构的逐渐退化。IGBT 模块封装结构的退化主要表现在模块的电学和热学性能的退化上。

1.1 热退化

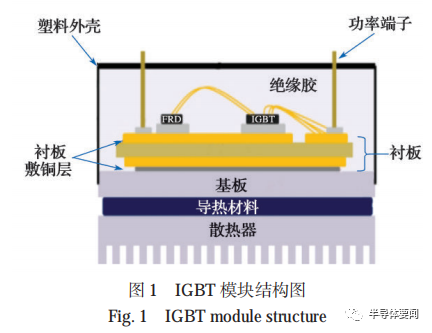
IGBT 模块（结构图见图 1）在应用中的电压、电流不是恒定的，而是随着汽车运行速度和载荷的变化而变化，从而使模块温度不断变化。由于模块芯片、芯片焊层、DBC 等层次的热膨胀系数不完全一致，当模块受到芯片温度的循环冲击时，不同材料会产生不同程度的受热膨胀和冷却收缩，从而使模块的各层材料之间产生交变的应力，造成结构的松弛和材料裂纹的萌生，使得导热系数等热参数退化。当 IGBT 模块的焊料出现裂纹和分层时，从芯片到模块底部散热器之间的有效传热面积就会减小，造成模块热阻 Rth 的增大。IGBT 模块热阻的增大又会降低模块的传热性能，导致芯片结温 Tj 升高。

1.2 电参数退化

在应用工况中，IGBT 模块材料的损伤会影响其外部电学特性，使模块的电气参数发生变化，这些电气参数包括压降 VCE(sat)和 VF、栅极阈值电压 VGE(th)、栅极电流 IGES 等。键合线与芯片之间热膨胀系数不匹配引起的热应力会造成键合线脱落，导致键合线接触电阻增大，进而使得 IGBT 模块的导通电阻 Ron 增大，饱和压降 VCE (sat)升高。此外，为了连接 IGBT 芯片元胞和发射极，进行芯片与衬板的引线键合，芯片表面会覆盖一层镀层金属。当镀层金属受到温度冲击时，晶粒会产生塑性变形 ，引起金属化重构。镀层金属的演化会减小其有效横截面积，增大整个镀层金属的电阻，影响模块的饱和压降 VCE(sat)。

2 键合热机仿真

IGBT 模块工作过程中涉及到电流场、温度场、应力场等多个物理场相互作用的影响，电流场产生功率损耗，功率损耗引起的焦耳热是温度场中的热源，模块温度的波动及温度场的不均匀分布会使模块各层之间产生热应力，进而模块发生形变。模块形状的改变又会引起温度场的变化和电流分布的改变，因此，在进行 IGBT 模块键合线应力仿真时，应考虑多个物理场之间相互耦合的情况。本文建立的 IGBT 模块实体模型如图 2 所示。在芯片表面有源区施加发热载荷，模拟芯片发热时的温度场分布，计算键合线的累积塑性变形损伤及其具体发生的位置。

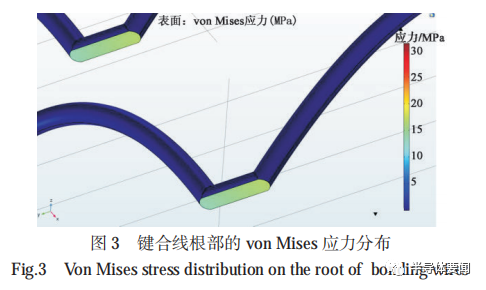
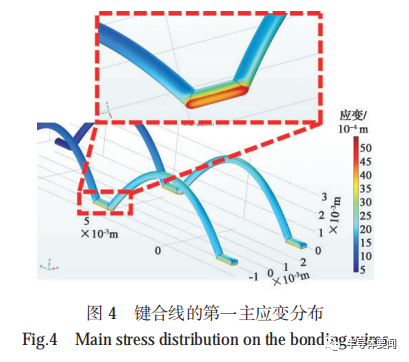
图 3 给出了键合线根部的 von Mises 应力分布。可以发现，在键合点处产生 von Mises 应力的最大值，键合线根部出现应力集中现象。提取键合线上的第一主应变分布，如图 4 所示，发现在应力较大的键合线根部位置键合线的第一主应变最大。功率循环试验中IGBT 模块键合线的失效，往往是在键合点处产生裂纹，裂纹扩展导致键合线脱落。

3 试验设计

3.1 功率循环试验方法

大功率 IGBT 模块功率循环常用的试验方法有恒定结温升ΔTj 、恒定功率 P 和恒定电流 IC。恒定结温升ΔTj 和恒定功率 P 主要是针对焊层的退化，其中恒定结温升ΔTj 的试验模式更加普遍；恒定电流 IC 试验模式则主要用于评价键合点的寿命。

3.1.1 恒定结温升 ΔTj 模式

恒定结温升 ΔTj 试验模式即在试验过程中，Ton 和Toff 保持不变，实时调整 IC 的值，使ΔTj 恒定。该试验模式下，随着产品热特性的退化，维持结温升ΔTj 稳定需要不断地减小电流 IC。恒定结温升 ΔTj 的试验模式在轨道交通用高压 IGBT 模块的芯片焊层热疲劳评价中被广泛应用。对于轨道交通用 IGBT 模块通常会对引线键合点进行涂胶保护，引线不会轻易脱落，其寿命短板为芯片焊层的分层和收缩。结温变化值是焊层热疲劳退化的主要因子，受电流大小影响较小，故轨道交通用高压IGBT 模块试验采用恒定结温升ΔTj 的模式比较合适。

3.1.2 恒定电流 IC 试验模式

恒定电流 IC 试验模式即为在试验过程中，Ton, Toff,IC 全部保持不变。在试验开始的时候通过前期调整使Ton, Toff, IC 满足设定的ΔTj 的要求，在试验过程中不再对这些参数进行调节。这种试验模式下，随着产品热退化和电退化综合效应导致ΔTj 越来越大。对于汽车用IGBT 模块，由于封装工艺和材料等与高压模块存在差异且考虑成本因素，对模块的引线键合点通常未涂覆保护胶，键合点是 IGBT 模块寿命的短板，电参数退化是主要的退化原理，通常采用恒定电流 IC 模式进行试验。AQG324 汽车模块标准也做了同样的规定说明。

3.1.3 热敏系数测试

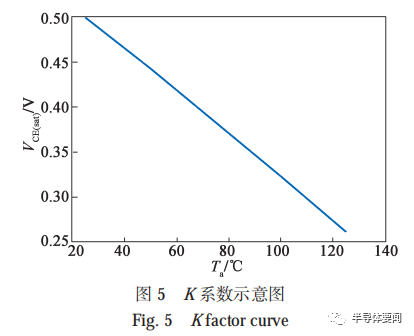
在进行功率循环前，试验人员需要对 IGBT 模块进行热敏系数（也称 K 系数）的测量。在小电流下，结温和电压 VCE 呈线性关系。所以，在不同温度下对压降VCE 进行精准的标定，获取小电流下压降与温度的关系曲线，该曲线的斜率即为 IGBT 的 K 系数，K 系数示意图见图 5。试验过程中只需获取小电流下模块的压降即可反推出芯片的结温。

3.2 威布尔统计方法介绍

威布尔分布在可靠性工程领域具有举足轻重的地位，该分布模型是功率半导体器件常用的寿命分布模型。本文研究的 IGBT 键合点失效主要由于材料寿命引起，其寿命分布可以用两参数威布尔统计分布来描述，其累积失效率计算公式为式中：

m 为形状参数；η为真尺度参数；N 为器件失效周期数。

将统计的键合点寿命数据进行整理，通过作图法，可以获得形状参数m和真尺度参数η的值，利用上述值，便可轻松算得样品的寿命为

式中：R 为规定的可靠度。

3.3试验方案设计

3.3.1 寿命模型

功率半导体寿命常用模型为

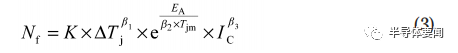
式中：Nf 为模块寿命；K 为玻尔兹曼常数；Tjm 为平均结温；EA 为激活能；β1, β2, β3 为计算值，与功率器件结构及材料有关，无实际物理意义。

对于功率IGBT模块，式中的激活能EA通常取0.168eV 。上述模型中加速因子主要为ΔTj, Tjm, IC。本文以此模型为基础进行试验方案的设计。

3.3.2 试验设计

试验采用恒定电流 IC 的模式。对 ΔTj, Tjm, IC3 个加速因子进行拉偏试验，当对一个参数进行拉偏时，其他 2 个参数保持一致。拉偏方案具体见表 1~表 3。为满足设定的条件，可以适当调整 IGBT 栅极电压 VGE 和关断时间 Toff。

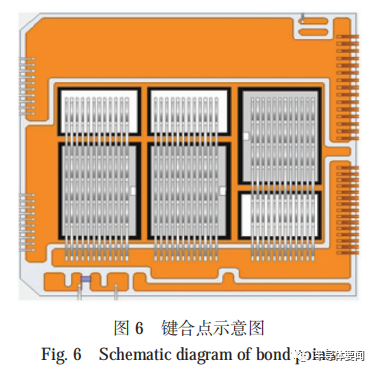
对于寿命分布的统计，通常都是取模块压降 VCE（sat）退化 5% 的循环次数作为模块的截止寿命 ，这种方式是将 IGBT 模块整体作为黑匣子处理，忽略了其失效的过程细节。在做寿命分布的时候需要大量的样本才能获取比较准确的寿命值，通常需要单个试验拉偏条件大于 10只的样本数量，这无疑需要巨大的经济成本和时间成本。针对汽车IGBT模块键合点脱落的失效模式，本文研究采用以键合点作为样本子样，进行功率循环寿命统计。图 6 所示模块是一种汽车用半桥 IGBT 模块，其一个桥臂有 144 个键合点，即每只模块可视为144 个样本子样，因此可以通过较少的几只模块的试验数据，得到大量键合点的寿命，这将大大减少试验的经济成本和时间成本，同时能够更准确获取键合点寿命的循环次数。

4 试验结果

4.1 试验数据统计

本文的试验设计采用恒定电流 IC 的试验模式。功率循环试验的热疲劳效应导致键合点与芯片金属层界面裂纹生长，每次键合点的脱落，IGBT 模块的压降VCE(on)会明显增大，形成一个明显的台阶，可以方便试验人员对键合点脱落时对应的循环周次数进行统计，如图 7 所示。

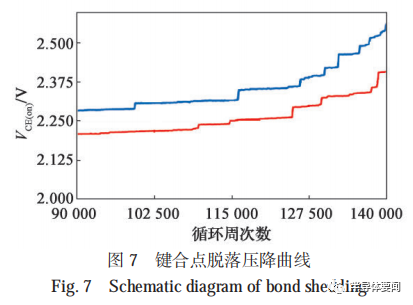
在键合点脱落数量较少的情况下，每个键合点的脱落会产生一个相对固定的 ΔVCE(on)。当键合点脱落数量达到一定数量后，每个键合点脱落会导致压降的增加值与初始的 ΔVCE(on)不再呈线性关系，影响到循环周次数对应的键合点脱落数量统计，可以采用定数截尾的方式进行试验来减小统计误差。每个压降突变处键合点的脱落数量可以近似计算为

式中：V2 为台阶上沿值；V1 为台阶下沿值；ΔVCE(on)为单根键合点脱落所增加的压降值。

随着产品性能的退化，芯片的温度也会大幅增加，IGBT芯片通常为正温度系数，可对式(4)进行系数修正，每个压降突变处键合点的脱落数量可近似计算为

根据试验过程曲线，按照式 (4) 或式 (5) 的计算方法，统计不同循环周次数对应的键合点脱落数量，如图 8 所示（图中点的个数即为键合点脱落数量）。

4.2 数据分析及寿命计算

按照威布尔分布计算方法对键合点脱落统计数据进行分析，获取在某一累计失效率下的 IGBT 模块功率循环寿命，如图 9 所示。威布尔参数计算方法已经非常成熟，本文不再赘述。

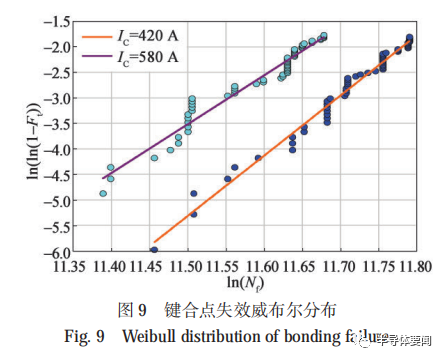
本文以键合点累积失效率为 10% 作为模块的寿命（也称为 B10寿命），计算得到不同试验条件下的IGBT 模块功率循环寿命，如表 4~表 6 所示。

基于寿命模型式(3)对上述试验数据代入进行计算，获取系数β1, β2, β3 值，通过计算的寿命模型可拟合得到在不同加速因子下的二维功率循环寿命曲线如图 10和图 11 所示。图 10和图 11 的曲线表明，IC 对键合点寿命的影响较大，是影响键合点寿命的主要加速因子；Tjm 对键合点寿命的影响相对较小，但也是影响键合点寿命的重要加速因子。失效模块解剖图如图所示 12。

对完成试验的模块进行解剖分析，模块键合点有明显剥离脱落，失效位置为键合点根部，佐证了前文的键合热机仿真的失效模式。

5结语

本文基于汽车 IGBT 模块功率循环寿命的研究，从失效原理、试验方法、寿命模型和统计模型等多个角度进行阐述，针对汽车 IGBT 模块的键合点寿命短板，进行了功率循环试验设计。本文提出基于键合点作为样本子样的寿命统计方法，相比传统以 IGBT 模块作为样本的寿命统计方法，该方法可以大幅度减少试验样本数量 , 节省巨大的时间成本和经济成本 , 并提升寿命评价的准确性，具有很好的工程应用价值。